Характеристика индуктивности в цепи переменного тока

Катушка индуктивности в цепи переменного тока

Если катушка индуктивности включена в цепь переменного тока, то в такой цепи, фаза тока всегда отстает от фазы напряжения. Разберем причины этого отставания на простейшем примере, когда в цепи имеется только индуктивное сопротивление, а омического сопротивления нет вовсе, или вернее омическим сопротивлением провода катушки самоиндукции можно пренебречь, так как оно мало.

Для удобства рассмотрения явлений будем считать, что мы присоединяем катушку индуктивности к источнику переменного тока в тот момент, когда напряжение U на его зажимах имеет максимальное амплитудное значение (рис. 1а.). Этот момент будем считать началом периода.

Рисунок 1. Самоиндукция-инерция. а) соотношения фаз тока, напряжения и ЭДС самоиндукции при включение катушки индуктивности в цепь переменного тока; б) соотношение фаз скорости движения, внешней силы и силы инерции

В момент включения катушки в ней немедленно возникнет электрический ток. Но ток не может сразу достичь своего амплитудного значения потому, что при его возникновении вокруг катушки начнет появляться магнитное поле, которое будет наводить в катушке ЭДС самоиндукции, направленную против внешнего напряжения, т. е. напряжения источника переменного тока. Электродвижущая сила самоиндукции будет препятствовать быстрому нарастанию силы тока в катушке. Поэтому нарастание тока будет длиться целую четверть периода.

По мере приближения к концу первой четверти периода скорость нарастания тока в катушке постепенно уменьшается.

Но вместе с тем ослабевает и ЭДС самоиндукции, так как величина ее зависит от скорости изменения силы тока.

Итак, в конце первой четверти периода внешнее напряжение, приложенное к катушке, будет равно нулю, ЭДС самоиндукции также будет, равна нулю, а ток в катушке и магнитный поток вокруг нее будут иметь максимальные амплитудные значения. В магнитном поле катушки будет запасено некоторое количество энергии, полученной от источника тока.

С началом второй четверти периода внешнее напряжение, переменив свое направление, будет возрастать, вследствие чего ток в катушке, текущий все еще в прежнем направлении, начнет уменьшаться. Но теперь в катушке снова возникнет ЭДС самоиндукции, обусловленная уменьшением магнитного потока, которая будет поддерживать ток в прежнем направлении.

В течение всей второй четверти периода внешнее напряже¬ние будет увеличиваться, а сила тока — уменьшаться. Ско¬рость уменьшения силы тока, оставаясь небольшой в начале второй четверти, станет постепенно нарастать и в конце этой четверти достигнет наибольшей величины.

Итак, к концу второй четверти периода внешнее напряжение приближается к амплитудному значению, а сила тока и магнитный ноток приближаются к нулю, убывая все с большей скоростью, вследствие чего ЭДС самоиндукции достигает своего амплитудного значения. Направление ЭДС самоиндукции, как всегда, остается противоположным направлению внешнего напряжения. Энергия, запасенная в магнитном поле за первую четверть периода, теперь возвращается обратно в цепь.

В течение второй половины (третья и четвертая четверти) периода все явления будут происходить в том же порядке, с той лишь разницей, что направления тока, внешнего напряжения и ЭДС самоиндукции изменяются на противоположные (рис. 1а.).

Таким образом, фаза тока все время отстает от фазы напряжения, причем нетрудно заметить, что сдвиг фаз тока и напряжения равен 90°.

Представим себе, что мы толкаем вдоль по рельсам груженую вагонетку. В первый момент, когда вагонетка только начинает трогаться с места, мы прилагаем к ней максимум усилий, которые по мере увеличения скорости вагонетки будем постепенно уменьшать. При этом мы почувствуем, что вагонетка, обладая инерцией, как бы сопротивляется нашим усилиям. Это противодействие (реакция) вагонетки будет особенно сильным вначале, по мере же ослабления наших усилий будет ослабевать и противодействие вагонетки, она постепенно будет переставать «упрямиться» и покорно покатится по рельсам.

Затем мы вовсе перестанем толкать вагонетку и даже, наоборот, начнем понемногу тянуть ее в обратном направлении. При этом мы почувствуем, что вагонетка снова сопротивляется нашим усилиям. Если мы будем все сильнее и сильнее тянуть вагонетку назад, то и ее противодействие будет соответственно все более и более возрастать. Наконец, нам удастся остановить вагонетку и даже изменить направление ее движения. Когда вагонетка покатится обратно, мы будем постепенно ослаблять наши усилия, т. е. будем тянуть ее все слабее и слабее, однако, несмотря на это, скорость вагонетки будет все-таки увеличиваться (при слабом трении в подшипниках).

Когда вагонетка пройдет половину пути в обратном направлении, мы совсем перестанем тянуть ее и снова переменим направление наших усилий, т. е. начнем ее снова задерживать, постепенно увеличивая силу торможения до тех пор, пока вагонетка не остановится, заняв первоначальное (исходное) положение. После этого мы можем продолжать все наши действия сначала.

В этом примере наши усилия, прилагаемые к вагонетке, соответствуют внешней ЭДС, противодействие вагонетки, обусловленное ее инерцией, — ЭДС самоиндукции, а скорость вагонетки — электрическому току. Если изобразить графически изменение наших усилий, а также изменение противодействия вагонетки и ее скорости с течением времени, то мы получим графики (рис. 1б), в точности соответствующие графикам рис.1а.

Из этого примера становится более понятной сущность реактивного (безваттного) сопротивления. В самом деле, в течение первой четверти периода мы толкали вагонетку, а она противодействовала нашим усилиям; в течение второй четверти периода она катилась сама, а мы «упирались»; в течение третьей четверти периода мы опять тянули ее, а вагонетка снова оказывала противодействие нашим усилиям и, наконец, в течение четвертой четверти периода она снова катилась сама, а мы ее тормозили.

Короче говоря, в течение первой и третьей четверти периода мы работали «на вагонетку», а в течение второй и четвертой четвертей она работала «на нас», возвращая обратно полученную то нас энергию. В результате наша работа оказалась «безваттной».

Таким образом катушка индуктивности в цепи переменного тока может работать как безваттный резистор.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

§51. Индуктивность в цепи переменного тока

Ток, напряжение и э. д. с. самоиндукции. При включении в цепь пременного тока индуктивности (катушки индуктивности, потерями в которой можно пренебречь) (рис. 178, а) изменяющийся ток непрерывно индуцирует в ней э. д. с. самоиндукции

e_L = -L ?i / ?t (68)

где ?i/?t— скорость изменения тока.

Рассматривая график изменения силы тока i (рис. 178,б), можно установить, что скорость его изменения ?i/?t будет наибольшей в моменты времени, когда угол ? равен 0; 180 и 360°. Следовательно, в эти минуты времени э. д. с. имеет наибольшее значение. В моменты времени, когда угол ?t равен 90° и 270°, скорость изменения тока ?i/?t = 0 и поэтому э. д. с. e_L = 0.

Э. д. с. самоиндукции е согласно правилу Ленца направлена так, чтобы препятствовать изменению тока. Поэтому в первую четверть периода, когда ток i увеличивается, э. д. с. e_L имеет отрицательное значение (направлена против тока); во вторую четверть периода, когда ток i уменьшается, э. д. с. e_L имеет положительное значение (совпадает по направлению с током). В третью четверть периода ток i изменяет свое направление и увеличивается, поэтому э. д. с. самоиндукции e_L направлена против тока и имеет положительное значение. В четвертую четверть периода ток i уменьшается и э. д. с. самоиндукции e_L стремится поддержать прежнее направление тока, т. е. имеет отрицательное значение. Таким образом, э. д. с. самоиндукции e_L отстает по фазе от тока i на угол 90°.

Так как в цепи, куда включена индуктивность L, отсутствует активное сопротивление (рассматривается идеальная катушка индуктивности), то по второму закону Кирхгофа u+e_L=0, т. е. u = -e_L Следовательно, напряжение источника всегда равно по величине и противоположно по направлению э. д. с. самоиндукции.

Из рассмотрения кривых (см. рис. 178,б) видно, что кривая напряжения и сдвинута относительно кривой силы тока i на четверть периода, т. е. на угол 90°. При этом напряжение достигает наибольших и нулевых значений раньше, чем ток. Следовательно,

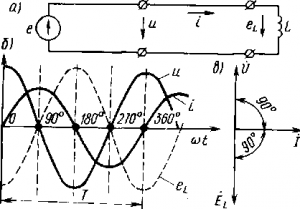Рис. 178. Схема включения в цепь переменного тока индуктивности (а), кривые тока I, напряжения и, э.д.с. e_L (б) и векторная диаграмма (в)

при включении в цепь переменного тока индуктивности ток i отстает по фазе от напряжения и на угол 90° или, что то же самое, напряжение и опережает ток по фазе на угол 90° (рис. 178, в).

Индуктивное сопротивление. Сопротивление катушки или проводника переменному току, вызванное действием э. д. с. самоиндукции, называется индуктивным сопротивлением. Оно обозначается X_L и измеряется в омах. Физическая природа индуктивного сопротивления совершенно другая, чем активного. Э. д. с. самоиндукции e_L направлена против приложенного напряжения u, которое заставляет изменяться ток; согласно закону Ленца она препятствует изменению тока i, т. е. оказывает прохождению переменного тока определенное сопротивление.

Чем большая э. д. с. самоиндукции e_L индуцируется в проводнике (катушке), тем большее они имеют индуктивное сопротивление X_L. Э. д. с. самоиндукции согласно формуле (68) прямо пропорциональна индуктивности L и скорости изменения тока ?i/?t, т. е. частоте его изменения f (значению ?). Поэтому индуктивное сопротивление

Следовательно, индуктивное сопротивление не зависит от материала, из которого изготовлен проводник (катушка), и от площади поперечного сечения проводника.

Закон Ома для цепи с индуктивностью

Электрическая мощность. Рассмотрим, как изменяется электрическая мощность в цепи переменного тока с индуктивностью. Мгновенное значение мощности р, равное произведению мгновенных значений силы тока i и напряжения и, можно получить графическим путем, перемножая ординаты кривых тока и напряжения при различных углах ?t. Кривая мгновенной мощности р (рис. 179, а) представляет собой синусоиду, которая изменяется с двойной частотой 2? по сравнению с частотой изменения тока i и напряжения и.

При рассмотрении этой кривой видно, что мощность р может иметь положительные и отрицательные значения. В течение первой четверти периода ток и напряжение положительны и мощность p = ui также положительна. Во второй четверти периода ток положителен, а напряжение отрицательно; следовательно, мощность р будет отрицательна. В течение третьей четверти периода мощность снова становится положительной, а в течение четвертой четверти — отрицательной.

Понятие положительной и отрицательной электрической мощности физически определяет направление потока энергии. Положительный знак мощности означает, что электрическая энергия W передается от источника к приемнику; отрицательный знак мощности означает, что электрическая энергия W переходит от приемника к источнику. Следовательно, при включении в цепь переменного тока индуктивности возникает непрерывный колебательный процесс обмена энергией между источником и индуктивностью, при котором не создается никакой работы. В первую и третью четверти периода мощность положительна, т. е. индуктивность получает энергию W от источника (см. стрелки W) и накапливает ее в своем магнитном поле. Во вторую и четвертую четверти периода индуктивность отдает накопленную энергию W источнику. При этом протекание по цепи тока поддерживается благодаря действию э.д. с. самоиндукции e_L.

Таким образом, в целом за период в индуктивное сопротивление не поступает электрическая энергия (на это указывает то, что среднее значение мощности за период равно нулю). Для того чтобы подчеркнуть указанную особенность индуктивного сопротивления, его относят к группе реактивных сопротивлений, т. е. сопротивлений, которые в цепи переменного тока в целом за период не потребляют электрической энергии. Следует отметить, что в реальные катушки индуктивности поступает некоторая энергия от источника переменного тока из-за наличия активного сопротивления проводов, из которых выполнены эти катушки. Эта энергия превращается в тепло.

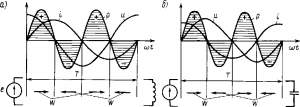Рис. 179. Кривые тока i, напряжения u и мощности р при включении в цепь переменного тока катушки индуктивности (а) и конденсатора (б)

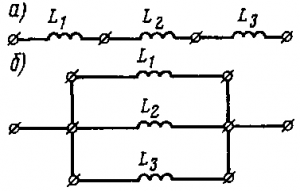Рис. 180. Последовательное (а) и параллельное (б) соединения катушек индуктивности

Так как среднее значение мощности в цепи с индуктивностью равно нулю, для характеристики процесса обмена энергией между источником и индуктивностью введено понятие реактивной мощности индуктивности:

где U_L — напряжение, приложенное к индуктивности L (действующее значение).

Реактивная мощность измеряется в варах (вар) и киловарах (квар). Наименование единицы происходит от первых букв слов вольт-амперреактивный. Реактивную мощность можно выразить также в виде

Q_L = U 2 L/X_L или Q_L = I 2 X_L

Способы соединения катушек индуктивности. В цепях переменного тока приходится соединять катушки индуктивности последовательно и параллельно.
При последовательном соединении катушек индуктивности эквивалентная индуктивность L_эк равна сумме индуктивностей; например, при трех катушках с индуктивностями L₁, L₂ и L₃ (рис. 180, а)

В этом случае эквивалентное индуктивное сопротивление

При параллельном соединении катушек индуктивности (рис. 180,б) для эквивалентной индуктивности имеем:

для эквивалентного индуктивного сопротивления

Катушка индуктивности: параметры и характеристики.

Индуктивность в цепи постоянного тока

Для лучшего понимания происходящих процессов в катушке, рассмотрим, что происходит в катушке при подаче на нее постоянного напряжения.
При подключении источника питания к катушке в ней начинает протекать ток, который создает вокруг неё магнитное поле.
Магнитные силовые линии поля распространяются через витки катушки наружу пересекая их, и образуют при этом ЭДС самоиндукции.
Эта ЭДС, согласно правилу Ленца, будет препятствовать мгновенному нарастанию тока в катушке. Нарастание тока происходит постепенно, по экспоненциальному закону.
Через небольшой промежуток времени переходной процесс заканчивается, и ток достигает своего нормального значения.
Продолжительность нарастания тока в секундах определяется по формуле:

где L — индуктивность катушки в генри , а R — общее сопротивление всей цепи в омах .
Если, к примеру, индуктивность катушки L=0,6 Г, а сопротивление цепи R=60 Ом, тогда длительность переходного процесса будет равна:
t=3•0,6/60=0,03 сек.

При отключении батареи от катушки индуктивность тоже происходит переходный процесс (такой опыт с первичной обмоткой трансформатора показан на странице «Электромагнетизм» рис.е).
В этом случае силовые магнитные линии будут приближаться к центру катушки опять пересекая ее витки. Создается ЭДС самоиндукции, которая уже направлена не против тока, а (опять же по правилу Ленца) совпадающая с направлением прерванного тока.

Если катушка имеет большую индуктивность (в нашем опыте катушкой является первичная обмотки трансформатора с большим количеством витков и значительным железным сердечником) и через нее протекал большой ток, то тогда ЭДС самоиндукции, появляющая на концах катушки индуктивности, может достигать величины во много раз больше напряжения источника питания.
Это объясняется тем, что при размыкании питающей сети энергия, запасенная в магнитном поле катушки, не исчезает, а превращается в ток.
Напряжение между концами катушки индуктивности может достигать таких значений, которое способно привести к пробою между обмотками, а так же выводу из строя полупроводниковых приборов. Это надо надо учитывать на практике при работе с приборами, имеющие катушки с большой индуктивностью через которые проходит значительный ток.

Индуктивность в цепи переменного тока

Для опытов с постоянным током катушка индуктивности намотана тонким проводом с большим количеством витков.
Это делается для того, чтобы при подаче на нее напряжения с мощного источника питания витки катушки не перегорели, т.к. при намотке витков толстым проводом сопротивление будет маленьким, а ток через нее большой (по закону Ома для постоянного тока I=U/R) и она может сгореть.
Сопротивление катушки индуктивности постоянному току (которое можно измерить мультиметром) называется активным сопротивлением.

Будет иначе, если в цепь катушки подать переменный ток.
При этом магнитное поле катушки индуктивности становится тоже переменным.
На рисунке показано, как меняется магнитное поле при синусоидальном токе. Во время периода магнитное поле меняет как свою силу, так и свое направление по синусоидальному закону. А это значит, что при этом возникает ЭДС самоиндукции, которая, согласно правилу Ленца, будет препятствовать приложенному извне напряжению.

Рассмотрим график происходящих процессов в катушке индуктивности.
При включения катушки в цепь переменного тока в первую четверть периода ( 0º-90º ) на катушку поступает нарастающее напряжение и ее магнитное поле «расширяется», накапливая магнитную энергию. Ток, в этот момент, противодействующей ЭДС самоиндукции, максимальный и противоположный по знаку с напряжением на катушке.
За другую четверть периода ( 90º-180º ), когда напряжение на катушке индуктивности уменьшается, магнитное поле «сворачивается», индуцируя ЭДС самоиндукции, которое совпадает с направлением тока. Этот ток самоиндукции в катушке старается уже «помочь» уменьшающему переменному току сохранить достигнутый большой магнитный поток. В этот полупериод катушка индуктивности уже не потребляет, а отдает энергию обратно генератору.
Следовательно, происходит постоянный обмен энергий между генератором и катушкой. А это означает, что средняя мощность потребления катушки равна нулю.
Благодаря разнице фаз тока и напряжения в 90º, катушка индуктивности имеет реактивную мощность и, соответственно, реактивное сопротивление , как и конденсатор. Разница лишь в том, что в катушке индуктивности напряжение опережает ток, а в конденсаторе — наоборот.
Реактивное (индуктивное) сопротивление катушки, в отличии от ее активного сопротивления , не вызывает безвозвратных потерь энергии.

Допустим, возьмем идеальную катушку , в которой не учитываются сопротивления провода и другие потери.
Тогда катушка индуктивности окажет переменному напряжению индуктивное сопротивление XL ,которое измеряется в омах и вычисляется по формуле:

где f — частота тока в герцах (Гц), а L — индуктивность катушки в генри (Г).
Отсюда видно, что величина индуктивного сопротивления катушки зависит от частоты и индуктивности. Чем выше частота тока и больше индуктивность катушки, тем больше индуктивное сопротивление.

К примеру, найдем индуктивное сопротивление катушки индуктивностью 5Г на частоте 50Гц.
XL=2π•50•5=1570 Ом.
На частоте 1кГц эта катушка будет иметь индуктивное сопротивление 31кОм, а на 1МГц — 31МОм. На графике показана зависимость упомянутой катушки от частоты.

Теперь, зная значение индуктивного сопротивления, можно записать закон Ома при переменном токе через катушку:

Например,найдем ток, который протекает через идеальную катушку с индуктивностью L=500 мкГ, если ее подключить к переменному напряжению U=0,4 В и частотой f=500 кГц.
I= 0,4/2•3,14•5•10 3 •500•10 -6 =0,25 мА

В реальной катушке нужно учитывать не только индуктивное сопротивление, но и сопротивление потерь Rпот.
На низких частотах Rпот равно только сопротивлению провода катушки. При повышении частоты на катушке сопротивление потерь будет возрастать за счет появления других потерь (вихревые токи, поверхностный эффект проводника и т.д.) (рис. а ).
Поэтому полное сопротивление катушки индуктивности переменному току на средних частотах равно:

и называется импедансом.
На высоких частотах начинает оказывать еще влияние cобственная (паразитная) емкость катушки Спараз , которая шунтирует индуктивность (рис. b ).

Основными параметрами высокочастотных катушек индуктивности являются индуктивность, добротность и собственная емкость .
Индуктивность зависит от количества витков, размера катушки и наличия ферромагнитного сердечника. Чем больше намотано витков на катушке, тем больше ее индуктивность. А наличие сердечника увеличит индуктивность катушки.
Добротность определяет качество катушки индуктивности и равна отношению индукнивного сопротивления к сопротивлению потерь:

Чем больше добротность, тем качественнее катушка. Катушкой хорошего качества считается катушка с добротностью от 50 до 200.
Чтобы достигнуть такого качества используют следующие средства:
— применением сердечников, при которых увеличивается индуктивность при меньшем числе витков катушки (т.е. уменьшается сопротивление провода);
— увеличение толщины провода, что, правда, увеличит габариты катушки;
— в диапазоне длинных и средних волн применение провода литцендрат, который состоит из определенного количества проволочек изолированных друг от друга.
Собственная емкость катушки индуктивности обусловлена емкостью обмотки и является нежелательной. Для ее уменьшения применяются различные способы намотки катушки.
Одним из способов является перекрестная намотка типа «универсаль» (рис. c ). Так же применяется намотка витков не плотно друг к другу, а на определенном расстоянии с принудительным шагом)(рис. d,e ).

В помощь изучающему электронику

Формулы, вычисления, .

— Цепь переменного тока —

Данный справочник собран из разных источников. Но на его создание подтолкнула небольшая книжка «Массовой радиобиблиотеки» изданная в 1964 году, как перевод книги О. Кронегера в ГДР в 1961 году. Не смотря на такую ее древность, она является моей настольной книгой (наряду с несколькими другими справочниками). Думаю время над такими книгами не властно, потому что основы физики, электро и радиотехники (электроники) незыблемы и вечны.

Основные понятия

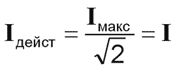
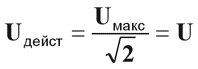
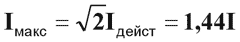
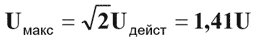
Сопротивление в цепи переменного тока

В омическом (активном) сопротивлении ток совпадает по фазе с напряжением (фазовый угол равен нулю), поэтому расчет сопротивления конструктивных элементов РЭА в цепях переменного тока производится по формулам, выведенным для цепи постоянного тока. По мере повышения частоты начинает проявляться так называемый поверхностный эффект, сопротивление проводника увеличивается, так как происходит вытеснение тока к поверхности проводника. Этот эффект характеризуется глубиной проникновения тока δ. Величина δ численно равна такому расстоянию от поверхности (проводника), на котором плотность тока составляет 36% от плотности тока на поверхности (уменьшается в e раз). Существенно, что, хотя сопротивление проводника увеличивается с ростом частоты, оно по-прежнему остается активным, ток и напряжение в проводнике совпадают по фазе. Глубина проникновения тока вычисляется по формуле

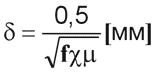
где:

Конденсатор в цепи переменного тока

Индуктивность в цепи переменного тока

С — емкость конденсатора С при настройке контура в резонанс на частоту генератора;
ΔС = С_В — С_Н — соответственно большее и меньшее, чем С, значения емкости конденсатора С, соответствующие уменьшению напряжения на контуре до 0,707 от резонансного значения.

При ω в 1/сек, и ΔС в ф,

8—длина воздушного зазора, см;
В — индукция, тл (обычно выбирают 5 = 0,7 тл);
I — ток, а.

Мощность переменного тока

Pa = U I cosφ [ва];

Pp = U I sinφ [ва];

Оглавление.

Основные понятия. Замкнутая и разветвленная цепи постоянного тока

Основные понятия, Сопротивление в цепи переменного тока , Конденсатор в цепи переменного тока, Индуктивность в цепи переменного тока, Мощность переменного тока

Основные зависимости, Последовательный колебательный контур, Параллельный колебательный контур

Входная цепь приемника

RC и LC фильтры — общие положения, RC фильтры, LC фильтры

Аттенюаторы, Согласование источника с нагрузкой по мощности, току и напряжению

Основные параметры передающих антенн, Параметры приемных антенн, Вибраторные антенны, Рамочные антенны, Приемные ферритовые антенны, Формулы для расчета вибраторных антенн

РАСПРОСТРАНЕНИЕ РАДИОВОЛН В СВОБОДНОМ ПРОСТРАНСТВЕ — Общие положения, ИОНОСФЕРА И ЕЕ ВЛИЯНИЕ НА РАСПРОСТРАНЕНИЕ РАДИОВОЛН, Преломление и отражение радиоволн в ионосфере, Особенности распространения сверхдлинных и длинных волн, Особенности распространения средних волн, Особенности распространения коротких волн, РАСПРОСТРАНЕНИЕ УЛЬТРАКОРОТКИХ ВОЛН В ПРИЗЕМНОМ ПРОСТРАНСТВЕ, Распространения радиоволн над поверхностью земли, дальний прием

Катушка индуктивности в цепи постоянного тока

Катушка индуктивности – это элемент характеризующимся своим свойством накапливать энергию магнитной поля.

Первый закон коммутации гласит: ток, протекающий в катушке индуктивности, в момент коммутации не может измениться скачком.

Это понятно из формулы:

Предположим, что ток iL изменился скачком, то есть:

А значит, что и напряжение в данном случае будет бесконечно велико:

Чего в природе быть не может, так как, следуя закону сохранения энергии, для этого бы потребовался источник энергии бесконечной мощности.

На схеме представлена RL – цепь, запитанная от источника постоянного тока. При замыкании ключа в положение 1, ток протекает по цепи “плюс” источника – резистор R – катушка индуктивности — “минус” источника. Тем самым, происходит накопление энергии магнитного поля в катушке индуктивности.

Напряжение и ток, протекающие в данной цепи, изменяются по экспоненциальному закону. Причем, их изменения взаимообратные, т.е. с увеличением тока, падение напряжения на катушке уменьшается.

Если мы переведем ключ в положение 2, то ток, не изменив своего направления, начнет уменьшаться по экспоненте до нуля. С физической точки зрения, в данном случае катушка отдает накопленную энергию магнитного поля в цепь, где она расходуется на тепловые потери в резисторе.

Одной из характеристик данной цепи является постоянная времени τ. Она зависит от величины индуктивности и активного сопротивления. Примерно за 5 τ ток в цепи достигает своего минимума или максимума.

Реализуем эту схему в программной среде Multisim 13.0 , взяв значения R = 10 Ом, L = 0,1 Гн.

Рассчитаем время, за которое ток в цепи достигает установившегося значения:

Собранная схема запитана от батареи 12 В. Для снятия значений тока, использовался инструмент “current probe”. Внутреннее активное сопротивление катушки индуктивности, принято равным нулю.

Индуктивность/катушка в цепи переменного тока — работа и влияние на цепь

При течении тока по проводнику всегда вокруг движущихся зарядов возникает магнитное поле. Для случая, когда в цепи имеется место с несколькими витками, вокруг них возникающее магнитное поле пронизывает собственный проводник, действуя как дополнительная ЭДС помимо основного источника питания. Под действием этой ЭДС в проводнике возникает ток самоиндукции, который в случае сети переменного напряжения также носит знакопеременный характер.

В соответствии с правилом Ленца, сила самоиндукции во всех случаях противодействует сите, вызвавшей её.

Поскольку ЭДС самоиндукции согласно данному условию противодействует изменениям в цепи, то в сети переменного тока этот фактор учитывается и обозначается как индуктивное сопротивление (ХL), измеряющееся аналогично активному сопротивлению в Омах.

Величина индуктивного сопротивления определяется величиной ЭДС самоиндукции, которая в свою очередь зависит от индуктивности катушки и частоты изменения напряжения в катушке.

где L — это индуктивность катушки, измеряется в Генриях (Гн);

ω — угловая частота переменного тока (рад/сек).

Другими словами, индуктивное сопротивление тем больше, чем выше частота протекающего переменного тока и чем большее количество витков имеется в катушке.

Катушки индуктивности в цепях переменного тока создают ток самоиндукции, который по фазе опережает напряжение в цепи на угол 90°. При этом в разные периоды изменения базового напряжения в катушке сначала происходит накопление энергии (при возрастании напряжения в любую сторону), а затем отдача её обратно в сеть (во время уменьшения напряжения в сторону нуля).

Таким образом, если пренебречь собственным активным сопротивлением проводника катушки, в среднем она не потребляет электроэнергию, а лишь изменяет характеристики и характер проходящего тока в цепи во времени.

То есть, вся запасённая в катушке в первый период энергия затем отдаётся обратно в электрическую сеть.

Это свойство позволило широко использовать катушки индуктивности в электротехнике для множества целей:

— в качестве основного накапливающего элемента в стабилизаторах, что позволяет преобразовывать уровни напряжения;

— несколько связанных между собой индуктивно катушек образуют трансформатор;

— в качестве электромагнитов;

— в радиосвязи для приёма и излучения электромагнитных волн (кольцевая антенна, магнитная антенна);

— для обнаружения магнитных полей;

— для нагрева проводящих ток материалов в печах индукционного типа и многое др.

При выборе подходящей для тех или иных целей катушки (индуктивности) необходимо учитывать частоту в сети, собственные характеристики катушки (резонансная частота, индуктивность, допустимый ток, накапливаемая мощность и т.д.).

Учебники

Разделы физики

Журнал «Квант»

Лауреаты премий по физике

Общие

Слободянюк А.И. Физика 10/18.5

§18. Переменный электрический ток

18.5 Индуктивность в цепи переменного тока. Индуктивное сопротивление.

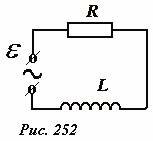
Исследуем теперь влияние индуктивности элементов цепей на протекание в них переменного электрического тока. Для этого рассмотрим электрическую цепь, состоящую из последовательно соединенных резистора с активным сопротивлением R и соленоида с индуктивностью L, подключенных к источнику переменной ЭДС (Рис. 252). Активным сопротивлением обмотки соленоида и внутренним сопротивлением источника пренебрежем. Последовательность описания процессов, происходящих в данной цепи, остается такой же, как и в предыдущих разделах.

Зависимость силы тока от времени описывается уравнением для мгновенных значений, которое следуют из закона Ома — суммарная ЭДС в контуре равна сумме напряжений на элементах контура:

varepsilon + varepsilon_ = IR) . (1)

В записи этого уравнения учтено, что при протекание переменного тока через катушку в ней индуцируется ЭДС самоиндукции, равная

varepsilon_ = -LI’) , (2)

где I′ — производная от силы тока по времени.

ЭДС самоиндукции в соответствии с правилом Ленца препятствует изменению силы тока в цепи. Поэтому для преодоления этого «сопротивляющегося» вихревого поля источник должен создавать в обмотке катушки потенциальное электрическое поле, разность потенциалов которого между концами обмотки должно быть по модулю равно ЭДС самоиндукции. Поэтому величину (

U_L = -varepsilon_) можно назвать напряжением на катушке индуктивности. Установим связь между силой тока в соленоиде и напряжением на нем. Для этого представим зависимость напряжения на катушке индуктивности от времени функцией

U_L = U_ cos omega t) . (3)

Тогда для нахождения зависимости силы тока от времени необходимо решить уравнение

U_ cos omega t = -varepsilon_ = LI’) . (4)

Этому удовлетворяет функция

I_L = frac> sin omega t = frac> cos left( omega t — frac <2>right)) , (5)

что можно проверить простой подстановкой этой функции в исходное уравнение [1] . Таким образом, амплитудное значение силы тока через соленоид связано с амплитудным значением напряжения простым соотношением

и между колебаниями силы тока и напряжения возникает разность фаз равная (

Delta varphi = -frac<2>). Эти результаты суммированы на рис. 253, где также представлена векторная диаграмма колебаний силы тока и напряжения.

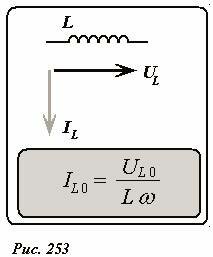
Выражение (6) совпадает по форме с уравнение закона Ома, поэтому величину (Z_L = L omega) разумно назвать индуктивным сопротивлением.

Физической причиной появления индуктивного сопротивления является ЭДС самоиндукции, препятствующая изменению тока через соленоид. Поэтому очевидно, что это сопротивление должно возрастать при возрастании частоты тока и при увеличении индуктивности цепи.

Проблема установления причинно-следственных связей между силой тока, ЭДС самоиндукции и напряжение в данном случае также относится к «философско-филологическим», то есть бессмысленной с физической точки зрения: электрическое поле, создаваемое источником, приводит к появлению переменного электрического тока, который посредством переменного магнитного поля создает ЭДС индукции, которая изменяет электрическое поле, которое влияет на протекание тока и так далее, как в сказке про попа и его собаку.

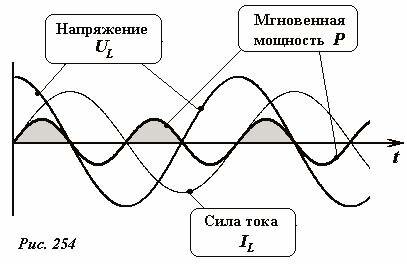
Так как между напряжением и силой тока существует разность фаз, равна (

Delta varphi = -frac<2>), то средняя мощность тока, протекающего через соленоид равна нулю. Следовательно, индуктивное сопротивление также является реактивным. На рис. 254 построены графики временных зависимостей напряжения, силы тока и мгновенной мощности тока через соленоид. Выделены промежутки времени, когда мощность тока положительна. В эти моменты энергия электрического тока переходит в энергию магнитного поля, создаваемого этим током в соленоиде. В других временных интервалах, когда индукция этого поля убывает, магнитное поле отдает свою накопленную энергию в цепь.

Наконец, построим векторную диаграмму для токов и напряжений в цепи, содержащей индуктивность (Рис. 252).

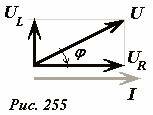
Так как сила тока в цепи одинакова, то построение диаграммы начнем именно с вектора, изображающего силу тока (Рис. 255). Затем строим векторы напряжений на резисторе U_R, параллельно вектору силы тока, и напряжения на соленоиде U_L перпендикулярно ему, в соответствии с рисунком 253. Сумма этих напряжений равна напряжению источника U. Используя теорему Пифагора и связь между амплитудами токов и напряжений, получим уравнение

U^2_0 = U^2_ + U^2_ = (I_0 R)^2 + (I_0 L omega)^2) , (7)

из которого определяем амплитудное значение силы тока в цепи

Из векторной диаграммы также определяем сдвиг фаз между силой тока и напряжением

Также с помощью векторной диаграммы несложно доказать, что и в данной цепи средняя мощность источника равна средней мощности теплоты, выделяющейся на резисторе.

Емкостное и индуктивное сопротивление в цепи переменного тока.

Емкостное сопротивление в цепи переменного тока

При включении конденсатора в цепь постоянного напряже­ния сила тока I=0, а при включении конденсатора в цепь пере­менного напряжения сила тока I ? 0. Следовательно, конденса­тор в цепи переменного напряжения создает сопротивление меньше, чем в цепи постоянного тока.

Мгновенное значение напряжения равно .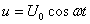

Мгновенное значение силы тока равно: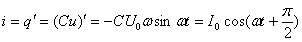

Таким образом, колебания напряжения отстают от колебаний тока по фазе на π/2.

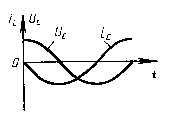
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению, то для максимальных значений тока и напряжения получим: 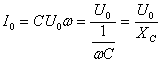, где 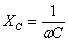— емкостное сопротивление.

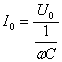
Емкостное сопротивление не является характеристикой проводника, т.к. зависит от параметров цепи (частоты).

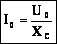
Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току).

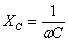
Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и емкостной нагрузкой. Такая нагрузка наз. реактивной.

Индуктивное сопротивление в цепи переменного тока

В катушке, включенной в цепь переменного напряжения, си­ла тока меньше силы тока в цепи постоянного напряжения для этой же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи посто­янного напряжения.

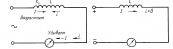
Мгновенное значение силы тока: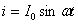

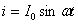
Мгновенное значение напряжения можно установить, учиты­вая, что u = — ε_i , где u – мгновенное значение напряжения, а ε_i – мгновенное значение эдс самоиндукции, т. е. при изменении тока в цепи возникает ЭДС самоиндукции, которая в соответствии с законом электромагнитной индукции и правилом Ленца равна по величине и противоположна по фазе приложенному напряжению.

.

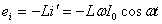Следовательно 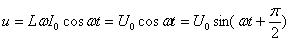, где 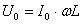амплитуда напряжения.

Напряжение опережает ток по фазе на π/2.

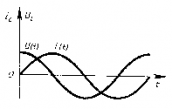
Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональная сопротивлению, то приняв величину ωL за сопротивление катушки переменному току, получим: — закон Ома для цепи с чисто индуктивной нагрузкой.

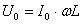
Величина 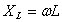— индуктивное сопротивление.

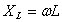
Т.о. в любое мгновение времени изменению силы тока противодействует ЭДС самоиндукции. ЭДС самоиндукции — причина индуктивного сопротивления.

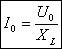
В отличие от активного сопротивления, индуктивное не является характеристикой проводника, т.к. зависит от параметров цепи (частоты): чем больше частота переменного тока, тем больше сопротивление, которое ему оказывает катушка.

Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и индуктивной нагрузкой. Такая нагрузка наз. реактивной.

Что такое катушка индуктивности и для чего она нужна

• Определение и принцип действия
• Виды и типы катушек
• Для чего нужны и какие бывают
• Основные параметры
• Маркировка

Определение и принцип действия

Катушка индуктивности — это катушка смотанного в спираль или другую форму изолированного проводника. Основные особенности и свойства: высокая индуктивность при низкой ёмкости и активном сопротивлении.

Она накапливает энергию в магнитном поле. На рисунке ниже вы видите её условное графическое обозначение на схеме (УГО) в разных видах и функциональных назначениях.

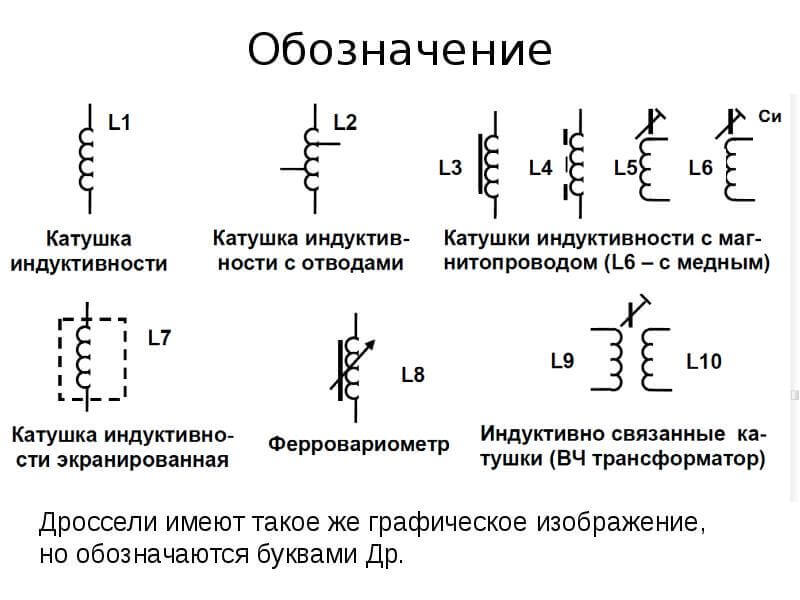
Она может быть с сердечником и без него. При этом с сердечником индуктивность будет в разы больше, чем если его нет. От материала, из которого изготовлен сердечник, также зависит величина индуктивности. Сердечник может быть сплошным или разомкнутым (с зазором).

Напомним один из законов коммутации:

Ток в индуктивности не может измениться мгновенно.

Это значит, что катушка индуктивности — это своего рода инерционный элемент в электрической цепи (реактивное сопротивление).

Давайте поговорим, как работает это устройство? Чем больше индуктивность, тем больше изменение тока будет отставать от изменения напряжения, а в цепях переменного тока — фаза тока отставать от фазы напряжения.

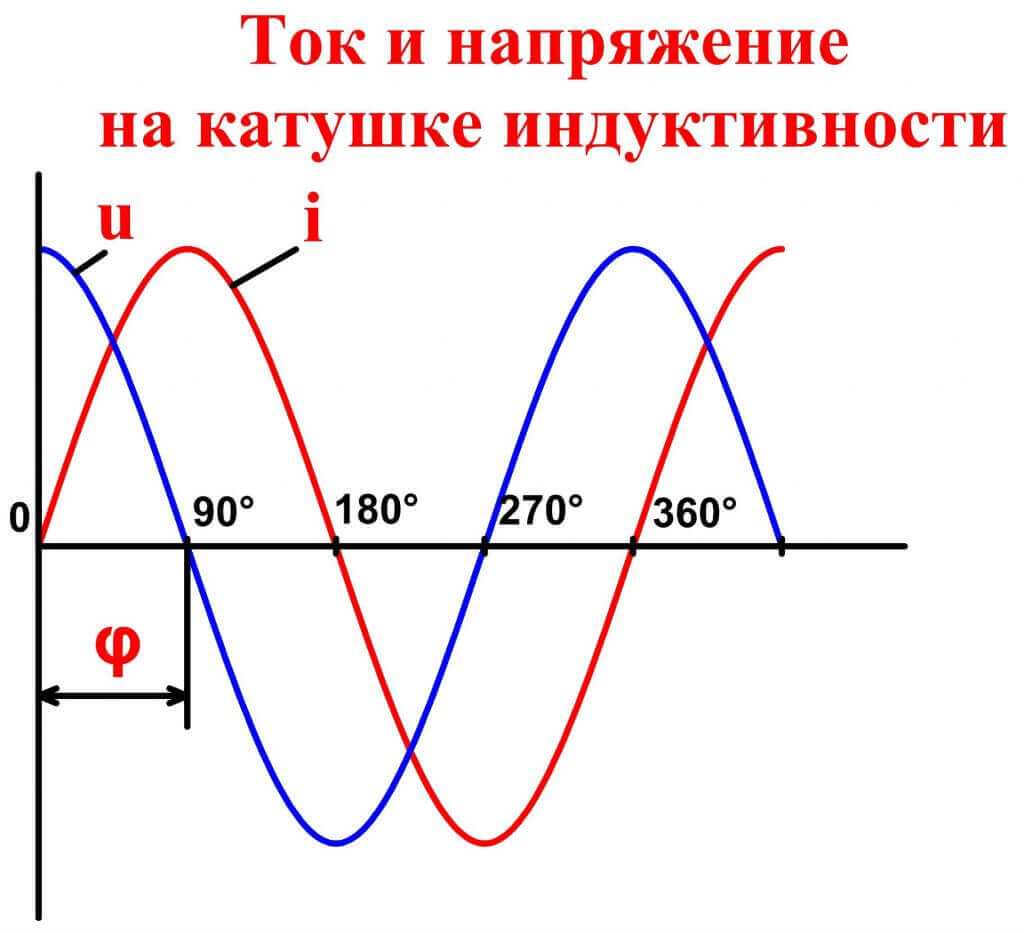
В этом и заключается принцип работы катушек индуктивности – накопление энергии и задерживание фронта нарастания тока в цепи.

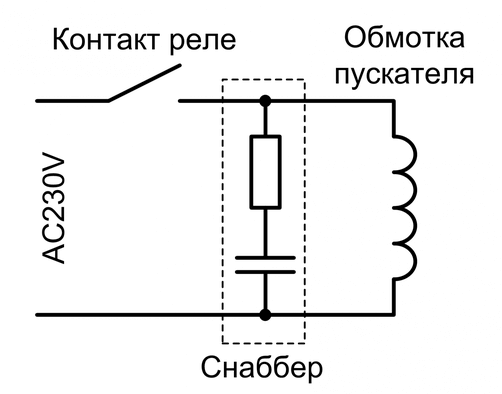
Из этого же вытекает и следующий факт: при разрыве в цепи с высокой индуктивностью напряжение на ключе повышается и образуется дуга, если ключ полупроводниковый — происходит его пробой. Для борьбы с этим используются снабберные цепи, чаще всего из резистора и конденсатора, установленного параллельно ключу.

Виды и типы катушек

В зависимости от сферы применения и частоты цепи может отличаться конструкция катушки.

По частоте можно условно разделить на:

• Низкочастотные. Пример — дроссель люминесцентной лампы, трансформатор (каждая обмотка представляет собой катушку индуктивности), реактор, фильтры электромагнитных помех. Сердечники чаще всего выполняются из электротехнической стали, для цепей переменного тока из листов (шихтованный сердечник).
• Высокочастотные. Например, контурные катушки радиоприемников, катушки связи усилителей сигнала, накопительные и сглаживающие дроссели импульсных блоков питания. Их сердечник изготавливают обычно из феррита.

Конструкция отличается в зависимости от характеристик катушки, например, намотка может быть однослойной и многослойной, намотанной виток к витку или с шагом. Шаг между витками может быть постоянным или прогрессивным (изменяющимся по длине катушки). Способ намотки и конструкция влияют на конечные размеры изделия.

Отдельно стоит рассказать о том, как устроена катушка с переменной индуктивностью, их еще называют вариометры. На практике можно встретить разные решения:

• Сердечник может двигаться относительно обмотки.
• Две обмотки расположены на одном сердечнике и соединены последовательно, при их перемещении изменяется взаимоиндукция и индуктивная связь.
• Сами витки для настройки контура могут раздвигаться или сужаться приближаясь друг к другу (чем плотнее намотка — тем больше индуктивность).

И так далее. При этом подвижная часть называется ротором, а неподвижная — статором.

По способу намотки бывают также различными, например, фильтры со встречной намоткой подавляют помехи из сети, а намотанные в одну сторону (согласованная намотка) подавляют дифференциальные помехи.

Для чего нужны и какие бывают

В зависимости от того, где применяется катушка индуктивности и её функциональных особенностей, она может называться по-разному: дроссели, соленоиды и прочее. Давайте рассмотрим, какие бывают катушки индуктивности и их сферу применения.

Дроссели. Обычно так называются устройства для ограничения тока, область применения:

• В пускорегулирующей аппаратуре для розжига и питания газоразрядных ламп.
• Для фильтрации помех. В блоках питания — фильтр электромагнитных помех со сдвоенным дросселем на входе компьютерного БП, изображен на фото ниже. Также используется в акустической аппаратуре и прочем.
• Для фильтрации определенных частот или полосы частот, например, в акустических системах (для разделения частот по соответствующим динамикам).
• Основа в импульсных преобразователях — накопитель энергии.

Токоограничивающие реакторы — используются для ограничения токов короткого замыкания на ЛЭП.

Примечание: у дросселей и реакторов должно быть низкое активное сопротивление для уменьшения их нагрева и потерь.

Контурные катушки индуктивности. Используются в паре с конденсатором в колебательном контуре. Резонансная частота подбирается под частоту приема или передачи в радиосвязи. У них должна быть высокая добротность.

Вариометры. Как было сказано — это настраиваемые или переменные катушки индуктивности. Чаще всего используются в тех же колебательных контурах для точной настройки частоты резонанса.

Соленоид — так называется катушка, длина которой значительно больше диаметра. Таким образом внутри соленоида образуется равномерное магнитное поле. Чаще всего соленоиды используются для совершения механической работы — поступательного движения. Такие изделия называют еще электромагнитами.

Рассмотрим, где используются соленоиды.

Это может быть активатор замка в автомобиле, шток которого втягивается после подачи на соленоид напряжения, и звонок, и различные исполнительные электромеханические устройства типа клапанов, грузоподъёмные магниты на металлургических производствах.

В реле, контакторах и пускателях соленоид также выполняет функцию электромагнита для привода силовых контактов. Но в этом случае его чаще называют просто катушка или обмотка реле (пускателя, контактора соответственно), как выглядит, на примере малогабаритного реле вы видите ниже.

Рамочные и кольцевые антенны. Их назначение — передача радиосигнала. Используются в иммобилайзерах автомобилей, металлодетекторах и для беспроводной связи.

Индукционные нагреватели, тогда она называется индуктором, вместо сердечника помещают нагреваемое тело (обычно металл).

Основные параметры

К основным характеристикам катушки индуктивности можно отнести:

1. Индуктивность.
2. Силу тока (для подбора подходящего элемента при ремонте и проектировании это нужно учитывать).
3. Сопротивление потерь (в проводах, в сердечнике, в диэлектрике).
4. Добротность — отношение реактивного сопротивления к активному.
5. Паразитная емкость (емкость между витками, говоря простым языком).
6. Температурный коэффициент индуктивности — изменение индуктивности при нагреве или охлаждении элемента.
7. Температурный коэффициент добротности.

Маркировка

Для обозначения номинала катушки индуктивности используют буквенную или цветовую маркировку. Есть два вида буквенной маркировки.

1. Обозначение в микрогенри.
2. Обозначение набором букв и цифр. Буква r – используется вместо десятичной запятой, буква в конце обозначения обозначает допуск: D = ±0.3 нГн; J = ±5%; К = ±10%; М = ±20%.

Цветовую маркировку можно распознать аналогично таковой на резисторах. Воспользуйтесь таблицей, чтобы расшифровать цветные полосы или кольца на элементе. Первое кольце иногда делают шире остальных.

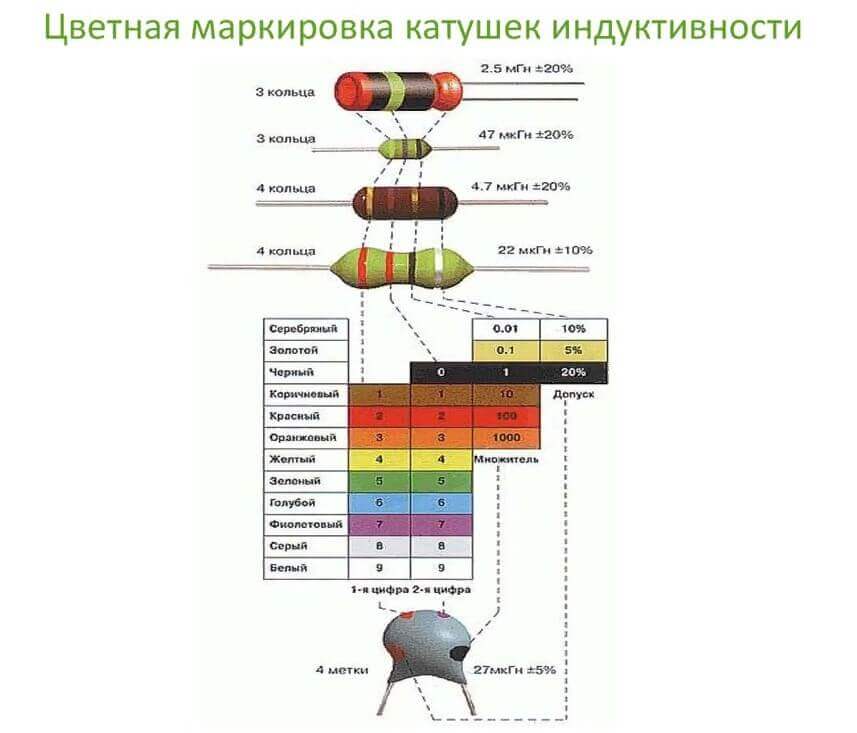
На это мы и заканчиваем рассматривать, что собой представляет катушка индуктивности, из чего она состоит и зачем нужна. Напоследок рекомендуем посмотреть полезное видео по теме статьи:

Материалы по теме:

Автор: Алексей Бартош