Особенности синусоидального тока
Московский государственный университет печати
Методические указания по выполнению контрольных работ по дисциплине «Электротехника и электроника»
для студентов обучающихся по специальности «Технология полиграфического производства»
В результате изучения данной темы студент должен
знать содержание терминов: резистор, сопротивление, индуктивность, индуктивное сопротивление, катушка индуктивности; емкость, емкостное сопротивление; фаза, начальная фаза, угол сдвига фазы; период, частота, угловая частота; мгновенное, действующее и среднее значения токов и напряжений; полные, активные, реактивные, комплексные сопротивления и проводимости; полная, активная, реактивная, комплексная мощности; основы символического метода моделирования цепей; законы Ома и Кирхгофа в символической форме; баланс мощностей для цепи синусоидального тока; условия и характеристики режимов резонанса в электрических цепях; законы электромагнитной индукции; методы расчета цепей с индуктивно связанными элементами;
уметь: выполнить анализ однофазной цепи синусоидального тока с любыми схемами соединений; построить векторные диаграммы токов и типографические диаграммы напряжений; правильно выбрать измерительные приборы и оценить их показания;
понимать: особенности электротехнических процессов в элементах и однофазных цепях синусоидального тока, сущность процессов в магнитосвязанных элементах.
1. Почему при анализе цепей синусоидального тока целесообразен символический метод, а не расчет по мгновенным значениям токов и напряжений?
2. Почему комплексные величины  » /> обозначают различным образом?
» /> обозначают различным образом?
3. Подчиняются ли комплексные величины  » /> одинаковым операциям с комплексными числами?
» /> одинаковым операциям с комплексными числами?
4. Почему нельзя непосредственно складывать сопротивления R = 1 Ом и X = 1 Ом?
5. Как зависят от частоты сопротивления резистора, индуктивности, емкости?
6. Для последовательной R-L-C цепи докажите подобие треугольников сопротивлений, напряжений, мощностей.
7. Для тока i = 10sin (314t + 30′) найти действующее значение, запишите комплекс действующего значения в алгебраической, тригонометрической и показательной формах, постройте вектор тока на комплексной плоскости.
8. Почему векторы напряжений и токов электрической цепи, вращающиеся с угловой частотой  » />, фиксируются на векторной диаграмме в их начальном положении?
» />, фиксируются на векторной диаграмме в их начальном положении?
9. Можно ли одну и ту же начальную фазу выразить и положительным, и отрицательным углом, и если можно, то как?
10. Как записать мгновенное значение суммарной ЭДС e(t) = 2sin (314t + 30°) + 5sin (314t — 150°)?
11. Вычислить комплексное Z и полное Z сопротивления ветви, содержащей последовательно соединенные резистор R = 4 Ом; индуктивное  » /> = 10 Ом и емкостное
» /> = 10 Ом и емкостное  » /> = 7 Ом сопротивления.
» /> = 7 Ом сопротивления.
12. В активно-индуктивной ветви напряжение по фазе опережает или отстает от тока?
13. В активном сопротивлении напряжение по фазе опережает, отстает или совпадает с током?
14. Вычислить активную мощность в цепи, если на входе  » />
» />
15. Определить характер сопротивления ветви и построить ее схему замещения, если в ней напряжение  » /> а ток
» /> а ток  » />.
» />.
16. Имеется ли различие в применении законов Кирхгофа для мгновенных и действующих значений токов и напряжений?
17. Как в эксперименте определить активное сопротивление катушки индуктивности? Как определить ее индуктивное сопротивление?
18. Можно ли трансформатор включать в сеть постоянного тока? И если нет, то почему?
19. Почему построение векторной диаграммы последовательной цепи целесообразно начинать с вектора тока?
20. В каком случае реактивное сопротивление цепи и сдвиг фаз между током и напряжением имеют отрицательный знак?
21. Может ли полное сопротивление цепи Z быть отрицательным?
22. Как изменить угол сдвига фаз?
23. Вычислить активную Р, реактивную Q и полную S мощности цепи, если  » />.
» />.
1. Касаткин А.С. и др. Электроника. — М.: Высшая школа, 2000.
2. Березкина Т. Ф. и др. Задачник по общей электротехнике и основам электроники. — М.: Высшая школа, 1998.
3. Электротехника и электроника: лаб. работы. — М.: МГУП, 2006.
4. Жаворонков М.А., Кузин А.В. Электротехника и электроника. — М.: ACADEMA, 2005.
Задание 2. Для электрической схемы, изображенной на рис. 2.1-2.50 , по заданным в табл. 2 параметрам и ЭДС источника определить токи во всех ветвях цепи и напряжения на отдельных участках. Составить баланс активной и реактивной мощностей. Построить в масштабе на комплексной плоскости векторную диаграмму токов и потенциальную диаграмму напряжений по внешнему контуру. Определить показание вольтметра и активную мощность, показываемую ваттметром.
Цепи синусоидального тока
Цепи синусоидального тока
Привет, мой друг, тебе интересно узнать все про цепи синусоидального тока, тогда с вдохновением прочти до конца. Для того чтобы лучше понимать что такое цепи синусоидального тока , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства
Современная электроэнергетика базируется в основном на переменном токе. Внедрение переменного тока в практику относится к 70-ым годам 19 века.
По сравнению с другими токами синусоидальный имеет ряд преимуществ, которые позволяют экономично осуществляет производство, передачу, распределение и использование электрической энергии. В настоящее время производство и передача электрической энергии осуществляются при помощи трехфазного тока с частотой 50 Гц во всех странах мира кроме США и Японии (60Гц).
Различные области техники используют широкий диапазон частот синусоидального тока, в зависимости от технических потребностей. Так в авиации применяют синусоидальный ток с частотой 400 Гц, так как при этом снижаются габаритные размеры и вес оборудования. В электротермических установках используют диапазон частот от 500Гц до 50МГц. Частоты от долей Гц до 10ГГц применяют в радиотехнике.
Но с использованием синусоидального тока появляются электромагнитные процессы, оказывающие влияние на электрические цепи более сложного характера, чем в цепях постоянного тока. Появляется ряд особенностей в работе, например, конденсатора и катушки индуктивности. Переменный ток порождает в этих элементах переменные электрическое и магнитное поля. В результате возникают явление самоиндукции в дросселе и токи смещения в конденсаторе, которые оказывают существенное влияние на процессы в сложных электрических цепях.
Параметры синусоидальных электрических величин
Синусоидальная функция является периодической функцией времени, т.е . Об этом говорит сайт https://intellect.icu . через равный промежуток времени, называемый периодом T, цикл колебаний повторяется.
i(t) = i(t + T), где i — мгновенное значение тока
Периоду Т соответствует фазовый угол 2π или 360°. Длительность времени периода Т измеряется в секундах.
Величина обратная периоду Т называют частотой и измеряется в Гц (число периодов в секунду)
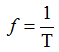
Также используется угловая частота ω =2πƒ (рад/сек) показывающая насколько фазовый угол синусоиды изменился за период, т.е. скорость изменения фазового угла синусоиды.
Аналитическое выражение мгновенных значений тока, ЭДС и напряжения определяется тригонометрической функцией:
i(t) = Im sin(ωt + ψi)
u(t) = Um sin(ω t + ψu)
e(t) = Em sin(ωt + ψe),
где Im, Um, Em – амплитудные значения тока, напряжения и ЭДС;
(ωt + ψ) – аргумент синуса, который определяют фазовый угол синусоидальной функции в данный момент времени t;Ψ – начальная фаза синусоиды, при t = 0
По ГОСТу ƒ = 50 Гц, следовательно, ω = 2πƒ = 314 рад/сек.
Временную функцию можно представить в виде временной диаграммы, которая полностью описывает гармоническую функцию, т.е. дает представление о начальной фазе, амплитуде и периоде (частоте). Временные диаграммы можно наблюдать с помощью специального прибора – осциллографа.
Рассмотрим пример:
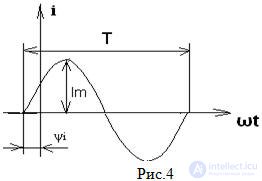
Функция тока i(t) сдвинута вправо от начала координат, это означает, что начальная фаза имеет отрицательный угол, ток появляется раньше на ψi относительно начала координат. Ток опережает начало координат
Но аналитическое выражение запишется следующим образом:
i(t) = Im sin(ωt + ψi),
Знак «+» или «–» перед начальной фазой показывает, сколько не хватает градусов, чтобы наша функция выходила из начала координат. Начальную фазу отсчитывают от начала синусоиды, при t = 0, до начала координат.
Все сказанное выше относится и к функциям напряжения u(t) и ЭДС e(t)
При рассмотрении нескольких функций электрических величин одной частоты интересуются фазовыми соотношениями, называемой углом сдвига фаз.
Угол сдвига фаз φ двух функций определяют как разность их начальных фаз φ = ψu — ψi
Если начальные фазы одинаковые, то φ = 0, тогда функции совпадают по фазе;
Если φ = ± π, то функции противоположны по фазе.
Особый интерес представляет угол сдвига фаз между напряжением и током рис.5
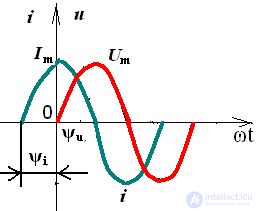
Рис.5
На практике используют не мгновенные значения электрических величин, а действующие значения. Действующим значением называют среднеквадратичное значение переменной электрической величины за период. Обозначается той же буквой, что и амплитудное значение, но без индекса.
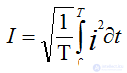
Для синусоидальных величин действующие значения меньше амплитудных в  раз, т.е.
раз, т.е.

Электроизмерительные приборы градуируются в действующих значениях.
Часто для технических расчетов необходимо знать среднее значение электрических величин, но его берут за половину периода, так как при определении среднего значения за период у синусоидальной функции получается 0.
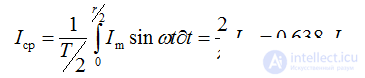
Следует обратить внимание на то, что среднее значение меньше действующего
Как ты считаеешь, будет ли теория о цепи синусоидального тока улучшена в обозримом будующем? Надеюсь, что теперь ты понял что такое цепи синусоидального тока и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятелно рекомендую изучить комплексно всю информацию в категории Электротехника, Схемотехника, Аналоговые устройства
Особенности синусоидального тока
Наиболее желательной формой кривой для мгновенных значений переменного тока и напряжения является синусоидальная форма.
Схема синусоидального тока.
В математике синусоидальные изменения считаются простейшей гармонической формой периодического процесса, поэтому расчет цепей синусоидального тока относительно прост и в таких цепях отсутствуют нежелательные побочные явления.

Рисунок 1. Построение синусоидальной кривой при помощи вращающего вектора.
Для построения синусоидальной кривой возьмем некоторый отрезок OA (рис. 1), длина которого в масштабе построения равна максимальному значению синусоидальной величины, — это вектор синусоидальной величины.
Например, Im = OA x n= 10 а, масштаб n = 0,1 а/мм; OA = 10 : 0,1 = 100 мм. В прямоугольной системе координат направим этот вектор сначала по горизонтальной оси — это будет исходное положение вектора в момент начала отсчета времени, т. е. при t = 0.
Вектор вращается с постоянной угловой скоростью против часовой стрелки. За время периода Т вектор поворачивается на 2? радиан (рад). Следовательно, его угловая скорость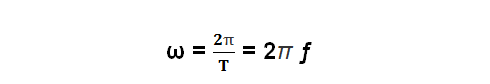
Так как в выражение ? входит частота переменного тока, то угловую скорость вектора обычно называют угловой частотой.
Когда с момента начала отсчета пройдет некоторое время t1 тогда вектор OA повернется на угол ?t1. Из конца вектора OA, находящегося в новом положении, опустим перпендикуляр на горизонтальную ось. Длина этого перпендикуляра будет OA x sin ?t1. В некоторый следующий момент t2 вектор образует с горизонтальной осью угол ?t2, а длина перпендикуляра, опущенного из его конца, будет, соответственно, OA хsin t2. Спустя четверть периода с момента начала отсчета времени, т. е. в момент t3 = T/4 вектор OA станет перпендикулярно к горизонтальной оси, а длина перпендикуляра
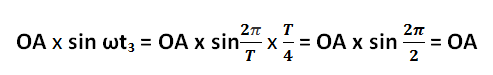

Рисунок 2. Синусоидальная величина с положительной начальной фазой.
Теперь рядом с окружностью, описываемой концом вращающегося вектора, построим в прямоугольной системе кривую зависимости величины OA х sin ?t от ?t или от t — это и будет синусоидальная кривая за промежуток времени от t = О до t = t3.
В момент t3 = T/4 синусоидальная величина достигает максимального значения. По мере дальнейшего вращения вектора величина OA х sin ?t убывает (моменты t4 и t5). Наконец, в момент t6 = T/2, описав дугу, равную ? радианам, вектор примет горизонтальное положение. В момент, когда OA х sin ?t6 = OA х sin ?=0“, синусоидальная величина проходит через нулевое значение.
При дальнейшем вращении вектора перпендикуляр OA х sin ?t будем считать отрицательным (моменты t7, ts, ts). Соответственно, построим вниз от горизонтальной оси этот участок синусоидальной кривой.
Если в начальный момент t = 0 вектор образует с горизонтальной осью некоторый угол а, то в момент начала отсчета синусоидальная величина не равна нулю, а имеет значение OA х sin 0 (рис. 2). Угол а называется начальным фазовым углом, или начальной фазой. В этом случае длина перпендикуляра, опущенного из конца вектора OA на горизонтальную ось в момент t, будет:
в соответствии с этим синусоидальная кривая в начальный момент не пройдет через нуль. Таким образом, в общем случае желательно, чтобы переменный ток изменялся во времени согласно выражению
В этом выражении i – мгновенное значение силы тока, Im — максимальное значение (амплитуда). Для получения синусоидального тока необходимо, чтобы ЭДС генераторов переменного тока была тоже синусоидальная,
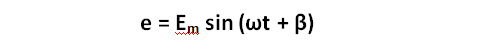
здесь ? – произвольная начальная фаза этой ЭДС. Если ЭДС е и ток i, относящиеся к одной и той же цепи, неодновременно проходят через нулевое или максимальное значение, то они сдвинуты по фазе относительно друг друга (рис. 3). При наличии сдвига фаз ЭДС в цепи может быть равна нулю, а ток еще будет в ней проходить, или же ток может быть равен нулю при наличии значительной ЭДС,

Рисунок 3. Сдвиг фаз между э. д. с. и током.
Сдвиг фаз ф измеряется разностью начальных фаз синусоидальных величин. В рассматриваемом нами случае ф = ? – а, причем ЭДС опережает по фазе ток. Соответственно, векторы Em и Im образуют угол ф, который остается неизменным при их вращении.
Синусоидальные величины, например напряжение и ток, совпадают по фазе, если их начальные фазы одинаковы; они же противоположны по фазе, если их сдвиг фаз ф = ± ?. Если одна из синусоидальных величин изменяется по синусоиде, например i = Im x sin ?t, а вторая — по косинусоиде, например u = Um cos ?t, то сдвиг фаз между ними ф = ? /2 (чему соответствует четверть периода), так как
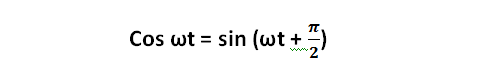
Необходимо иметь в виду, что вращающиеся векторы величин переменного тока существенно отличаются от векторов физических величин (силы, скорости, магнитной индукции, напряженности электрического поля и т. п.), имеющих определенное направление в пространстве.
Векторы переменного тока, называемые также радиус-векторами, представляют собой лишь удобную математическую форму изображения величин, изменяющихся во времени синусоидально. Радиус-векторы, как и пространственные векторы, часто кратко называют одинаково векторами. Векторы переменного тока отличают точкой над буквой, обозначающей ту или иную синусоидальную величину, например ?m или ?m
Исследование неразветвленной цепи синусоидального тока. Резонанс напряжений.
Главная > Реферат >Физика
Лабораторная работа №3
Исследование неразветвленной цепи синусоидального тока. Резонанс напряжений.
Цель работы : Изучение неразветвлённой цепи синусоидального тока, состоящей из последовательно соединенных R , L , С элементов, установление условий наступления резонанса напряжений в ней, определение её параметров.
Основные теоретические положения
Простейшая неразветвлённах цепь, состоящая из последовательно соединённых R , L , С элементов, приведена на рис. 1.
Электрическое состояние данной цепи определяется следующим уравнением, вытекающим из второго закона Кирхгофа:
где u = u ( t ) — мгновенное напряжение, приложенное к цепи;
u R , u L , u C , — мгновенные напряжения соответственно на R , L , С элементах;
i = i ( t ) — мгновенный ток, протекающий в цепи.
Анализ гармонических колебаний в линейных электрических цепях
проводится, как правило, относительно комплексных мгновенных токов ī и
напряжений ū , математические модели которых определяются следующими формулами:
— комплексные амплитуды тока и
напряжения, амплитуды и начальные фазы которых I m , U m и Ψ i , Ψ u
ω — угловая частота колебаний ī , ū , рад/с. Сравнивая ī с i и ū с u , находим,
где I т <. >— оператор выделения мнимой части комплексного числа (функции), стоящего(щей) в <>.
Тот факт, что ī к ū включают в себя i и u и являются их ( ī , ū ) изображениями на комплексной плоскости, математически записывается так:
где знак соответствия мгновенных величин их комплексным изображениям.
Уравнение (1) перепишем в виде:
Выполнив над ī предусмотренные уравнением (3) операции, получим:
Разделив обе части (5) на , окончательно получим:
Выражение (6) представляет собой закон Ома в комплексной форме.
В этом выражении:
— комплексное действующее значение напряжения ū ;
— комплексное действующее значение тока ī ;
— комплексное сопротивление R , L , С цепи;
1/ ω -С=Х C — ёмкостное сопротивление;
X = X L -Х C — реактивное сопротивление R , L , С цепи, которое в зависимости от соотношения L , С, ω может быть больше нуля ( Х L >Х C ) , меньше нуля (Х C >Х L ) , равно нулю ( X L = X C ) ;
-полное сопротивление R , L , С цепи;
— угол сдвига фаз между напряжением u и током i
Если в выражении (6) U и Ỉ относятся к участку цепи, то комплексное сопротивление этого участка. Например, в рассматриваемой цепи можно выделить шесть комбинаций участков (см. рис.2), комплексные сопротивления которых определяются следующими формулами:
для участка « R » — X = 0, Z R = R ;
для участка « L » — R = 0, X =Х L , Z L = j · X = j · X L ;
для участка «С» — R = 0, X =- X C , Z C = j · X =- j · X C ; (7)
для участка « R — L » — Z R — L = R + j · X ;
для участка « R — C » — Z R — C = R — j · X C ;
для участка « L — C » — Z L — C = j · ( X L — X C ) ;
Таким образом, с учетом приведенных формул действующие значения тока I и напряжении U R , U L , U C на участках цепи определяются следующими выражениями:
начальные фазы i , U R , U L , U C связаны между собой формулами:
Заметим, что для рассматриваемой цепи угол сдвига фаз между u и i
меньше нуля при x ;
больше нуля при х>0 ;
равен нулю при x= 0 .
Режим гармонических колебаний в цепи, состоящей из последовательно соединенных участков с разнохарактерными реактивными элементами, при котором φ =0 , называется резонансом напряжений .
Таким образом, условием возникновения резонанса напряжений является равенство нулю реактивного сопротивления цепи:
Для рассматриваемой цепи условие возникновения резонанса напряжений
можно получить путем изменения L , С , ω .
Например, при неизменных L , С резонанс наступит при частоте
С учетом (10) находим, что при резонансе:
— ток в цепи достигает максимально возможного значения
— напряжение на индуктивной катушке
— напряжение на конденсаторе
— напряжение на резисторе
В формулах (15), (16) величина
называется добротностью последовательного колебательного контура. В случае, когда , т.е. Q >1 , напряжения на индуктивной катушке и
конденсаторе при резонансе будут больше напряжения на входе цепи. По этой причине резонанс при последовательном соединении R , L , С элементов называют резонансом напряжений.
На рис.З приведены частотные (резонансные) характеристики I ( ω ), U L ( ω ), U C ( ω ) , U R ( ω ) , φ ( ω ) цепи (рис.1) при U = const . Векторная диаграмма цепи при резонансе показана на рис.4.
Для рассматриваемой цепи:
Отметим, что при резонансе напряжений реактивная мощность всей цепи
Следовательно, при резонансе напряжений колебания электрической энергии между источником и цепью нет, мгновенная мощность цепи ≥ 0 . Т.е. в этом режиме проходит непрерывное преобразование электрической энергии в тепловую.
Задание по работе
Экспериментально исследовать электрические цепи, состоящие из одного
пассивного элемента из возможных R , L , С .
По данным экспериментов (п.1) рассчитать параметры исследованных
цепей.
Экспериментально исследовать электрическую цепь, состоящую из последовательно соединенных R , L , С элементов при изменении емкости
конденсатора.
4. По данным эксперимента (п.З) построить резонансные кривые I (С) ,
U L ( C ) , U C ( C ) , φ ( C ) и рассчитать параметры цепи R , L , C .
5. Используя экспериментальные и расчетные данные (п. 3,4), построить в
масштабе на миллиметровой бумаге векторные диаграммы цепи для случаев
X , Х=0 , Х>0 .
Методические указания по выполнению работы
Ознакомиться с измерительными приборами и оборудованием панелей
лабораторного стенда, составить таблицы для внесения экспериментальных и
расчетных данных.
Собрать цепь, схема которой представлена на рис. 5,а . Установить наибольшее значение сопротивления переменного резистора и значение напряжения на входе цепи ≤ 50 В.
Напряжение устанавливается с помощью регулятора Атр. Частота напряжения сети f = 50 Гц. Произвести измерения действующих значений тока I , напряжения U , активной мощности Р цепи. Данные эксперимента завести в табл.1 (строка 1).
Собрать цепь, схема которой представлена на рис. 5,6 . При напряжении на входе цепи ≤ 50 В произвести измерения I , U , Р цепи. Данные эксперимента занести в табл. 1 (строка 2).
Собрать цепь, схема которой представлена на рис. 5,в . Величину емкости установить равной 20 мкФ. При напряжении на входе цепи ≤ 50 В произвести измерения I , U , Р цепи. Данные эксперимента занести в табл.1 (строка 3).
По данным опытов произвести расчет параметров схем ( рис 5,а,б,в ). Результаты расчетов занести в табл 1.
3. Собрать цепь, схема которой представлена на рнс.6. При напряжении на входе цепи U = 50 В подобрать емкость батареи конденсаторов C =С O , при которой ток в цепи будет максимальным. Записать показания приборов измерительного комплекта К-505 в табл. 2 (строка 4). Произвести измерения действующих значений напряжений на катушке U k и конденсаторе U c с помощью цифрового вольтметра; результаты измерений занести в табл. 2 (строка 4).
Произвести измерения I , U , P , U k U c для трёх значений ёмкости С С 0 и для трёх значений ёмкости С>С 0 . Результаты измерений занести в табл. 2 (строки 1-3,5-7).
При выполнении эксперимента действующие значения напряжения на входе цепи поддерживать постоянным (U=50 В).
По экспериментальным данным рассчитать параметры цепи для всех
значений емкостей C = C i , i =1,7 . Результаты расчетов занести в табл. 2.
4. На основании данных табл. 2 построить резонансные характеристики I ( C ) , U k (С) , U c ( C ) , φ (С) и векторные диаграммы цепи для случаев С 0 ; С= C 0 ; C > C 0 .
Задание на работу.
Схемы исследуемых целей и таблицы с экспериментальными и
расчетными данными.
4. Графики в векторные диаграммы, указанные в задании, построенные в масштабе на миллиметровой бумаге.
Каково условие возникновения резонанса напряжений и способы
его (условия) реализации на практике?
С помощью каких приборов можно судить о возникновении
резонанса напряжений?
Объясните характер изменения резонансных кривых?
Проведите анализ построенных векторных диаграмм.
Электротехника ТОЭ
Лекции и задачи по ТОЭ. На сайте представлен лекционный материал для изучения теоретических основ электротехники и видеоуроки по всем темам. Так же тут можно заказать решение задач, курсовых, расчетных, контрольных и домашних работ. Онлайн помощь на экзамене, контрольной. Решение тестов, занятия по скайпу и др. В ближайшее время на сайт будут добавлены готовые работы на разные темы ТОЭ, ТАУ и другим дисциплинам.
- Главная страница
- Теория
- Полезная литература
- Тесты по ТОЭ
- Заказать решение
- Познавательное
- Физика
- Готовые работы
- Цены
- Вопрос-ответ
4.2. Основные параметры синусоидального тока
Теория / 4.2. Основные параметры синусоидального тока
Анализ электрических цепей, в которых действуют сигналы любой формы, можно свести к анализу цепей с синусоидальными воздействиями. Поэтому изначально рассмотрим все особенности расчета цепей, относящиеся к синусоидальным токам и напряжениям, а затем обобщим их на цепи с другими видами воздействия.
Рассмотрим основные понятия, характеризующие переменный синусоидальный ток. Синусоидальный ток является периодическим. Пусть ток изменяется по закону синусов
График этой функции показан на рис. 4.3.
Дадим определение основным параметрам синусоидального тока.
Мгновенное значение – это значение тока в данный момент времени. Мгновенное значение меняется от точки к точке и обозначается строчной буквой i . Например, в момент времени t 1 мгновенное значение будет i 1 , в момент времени t 2 мгновенное значение будет i 2 .
Мгновенные значения переменного тока в течение одной половины периода положительны, а в другие полпериода отрицательны. Одно из двух возможных направлений тока в проводнике принимается условно за положительное направление, этому направлению соответствуют положительные мгновенные значения. И наоборот, другому направлению тока в проводнике будут соответствовать отрицательные мгновенные значения.
Введение понятия положительных направлений токов, ЭДС и напряжений необходимо, во-первых, для правильного составления уравнений Кирхгофа при расчете электрических цепей, а во-вторых – для анализа магнитных цепей, так как направление магнитных потоков зависит от направления токов в проводниках.
Амплитуда – наибольшее значение переменного тока. Амплитуда – это мгновенное значение, которое достигается в моменты времени, для которых угол
Амплитуда тока обозначается прописной буквой с индексом – Im . Аналогично обозначаются амплитуды напряжений – Um и ЭДС – Em .
Периодом Т называется наименьший промежуток времени, за который мгновенное значение тока, пройдя полный цикл, достигает первоначального значения. Период измеряется в секундах [ c ].
Частота переменного тока (циклическая) – величина, обратная периоду
Так как время Т измеряется в секундах, частота f измеряется в



