Мощности трехфазной симметричной системы

Примеры выполнения курсовых работ по электротехнике и электронике

Мощность трехфазной системы и ее измерение

Активная мощность трехфазной системы Р является суммой фазных активных мощностей, а для каждой из них справедливо основное выражение активной мощности цепей переменного тока. Следовательно, фазная активная мощность Рф = 3UфIфcos φ и при симметричной нагрузке активная мощность трехфазного устройства

Р = ЗРФ = 3 UфIф cos φ (3.7)

Но в трехфазных установках в большинстве случаев приходится выражать активную мощность устройства не через фазные, а через линейные величины. Это легко сделать на основании соотношений фазных и линейных величин, заменив в выражении активной мощности фазные величины линейными. При соединении звездой Uф = Uл / √3 ; 1Ф = Iл, а при соединении треугольником Uф = Uji; Iф = Iл/√3 .После подстановки этих выражений в формулу (3.7) получим одно и то же выражение для активной мощности трехфазной симметричной установки:

Хотя это выражение относится только к активной мощности симметричной системы, тем не менее им можно руководствоваться в большинстве случаев, так как в промышленных устройствах основная нагрузка редко бывает несимметричной.

Реактивная мощность в симметричной системе, так же как и полная мощность, выражается через линейные величины подобно активной мощности:

Простейшие условия измерения активной мощности трехфазной системы имеются в том случае, если фазы приемников соединены звездой с доступной нейтральной точкой. В этом случае для измерения мощности одной фазы цепь тока ваттметра соединяют последовательно с одной из фаз приемника (рис. 3.12 а), а цепь напряжения включают под напряжение той фазы приемника, в которую включена цепь тока ваттметра, т. е. зажимы цепи напряжения ваттметра присоединяются один к линейному проводу, а второй—к нейтральной точке приемника. В подобных условиях измеренная мощность

а мощность симметричного приемника

Часто нейтральная точка недоступна или фазы приемника соединены треугольником. Тогда применяется измерение с помощью искусственной нейтральной точки (рис. 12 6).

Такая точка (точнее узел) составляется из цепи напряжения ваттметра с сопротивлением rnm-n и двух добавочных резисторов С такими же сопротивлениями. При таком соединении цепь напряжения ваттметра находится под фазным напряжением, а через цепь тока прибора проходит фазный ток. Следовательно, и при таком измерении

Для измерения активной мощности в четырехпроводной установке (т. е. установке с нейтральным проводом) при несимметричной нагрузке применяют способ трех ваттметров (рис. 3.13). В такой установке каждый из ваттметров измеряет активную мощность одной фазы, а активная мощность установки определяется как сумма мощностей, измеренных тремя ваттметрами:

Если включить два ваттметра в трехпроводную систему постоянного тока (рис. 3.14), то они будут измерять мощность всей установки. При этом не имеет знамения, каковы напряжения отдельных пеней, объединенных в трехпроводную систем. Если вместо постоянных тока и напряжения рассматривать мгновенные значения напряжений и токов трехфазной системы, то в таких условиях ваттметры будут показывать средние значения мгновенных мощностей, т. е. активные мощности. Но следует иметь в виду, что хотя Р = Р1 + Р2, мощность системы равна сумме показаний двух ваттметров, но эта сумма алгебраическая, т. е. показание одного из ваттметров может быть отрицательным — стрелка одного из ваттметров может отклоняться в обратную сторону, за нуль шкалы. Чтобы отсчитать в таких условиях показание ваттметра нужно переключить зажимы цепи напряжения. Показания прибора после такого переключения следует считать отрицательными.

Рис. 3.14 Схема измерения активной мощности в трехфазной трехпроводной системе (способ двух ваттметров)

Пример. Трехфазный симметричный потребитель электроэнергии с сопротивлением фаз Za = Zь = Zc = Zф = R = 10 Ом соединен «звездой» и включен в трехфазную сеть с симметричным линейным напряжением Uл = 220 В (рис.3.15). Определить токи в фазных и линейных проводах, а также потребляемую активную мощность в режимах:

а) при симметричной нагрузке;

б) при отключении линейного провода;

в) при коротком замыкании той же фазы нагрузки.

Построить для всех трех режимов токографические диаграммы напряжений и показать на них вектора токов.

а) Решение. Фазные напряжения при симметричной нагрузке; Ua = Ub = Uc = Uф= Uл/√З = 220/√3 = 127 В. Фазные токи при этой нагрузке: IФ = Uф/Rф = 127/10 = 12,7 А. Линейные токи при симметричной нагрузке: IA = IС = Iл = Iф = 12,7 А, так как симметричный трехфазный потребитель электроэнергии соединен «звездой».

Активная мощность трехфазного симметричного потребителя: Р = ЗРф = ЗUф 1ф cos φ = 3*127*12,7* 1 = 4850 Вт = 4,85 кВт или Р = √5 Uл Iл соs φ _ф = √3*220*12,7*1 = 4850 Вт= 4,85 кВт, где cos φ _ф = 1 при Zф = Rф.

Векторная диаграмма напряжений и токов приведена на рис.3.16.

б)Решение Ток в линейных проводах аА и сС при обрыве линейного провода ЬВ (выключатель S разомкнут); так как сопротивление фазы Zb = ∞ (1В = 0), a Za = R и Zс = R включены последовательно на линейное напряжение UCa = Uл = 220 В; IA=1С = I = UcA/(R + R) = 220/(10 + 10) = 11 А.

Напряжение на фазах потребителя при обрыве линейного провода bВ (нейтральная точка и в этом случае соответствует середине вектора линейного напряжения UCA): Ua = Uc = UCA/2 = 220/2=110 В.

Напряжение между проводом фазы В и нейтральной точкой п определяют из векторной диаграммы (рис. 3.17): Uc = Uл cos pi/6 = 220* 0.866 = 190,5 В.

Активная мощность потребителя при обрыве линейного провода bВ: P = PA + РC = 2I2 Rф = 2*112*10 = 2420 Вт= 2,42 кВт.

в) Для условия задачи определить фазные напряжения Uф и токи 1Ф, активную мощность Рк потребителя при коротком замыкании фазы Zb, построить векторную диаграмму для этого случая рис. 3.18.

Решение. В данном случае Zb = 0 и Ub = 0, нейтральная точка п переместится в точку В, при этом фазные напряжения Uc = UBC, UA = Uав, т.е. фазные напряжения равны линейным напряжениям (Uф = Uл). При этом фазные токи: IA = Ic = Uл/R = 220/10 = 22 А. Ток 1В при коротком замыкании в соответствии с первым законом Кирхгофа для нейтральной точки n: IA + IB + IC = О или -IB = IA + Iс.

Из прямоугольного треугольника на векторной диаграмме рис. 3.19 имеем: (-IB/2)2 + (IA/2)2 = I2 А, откуда IB = √3 IA = √5 • 22 = 38 A. При этом 1А = Uл/Za = IC = Uл/Zc = Uл/R = 220/10 = 22 А.

Активная мощность цепи при коротком замыкании: Рк = РA + РC = 2 *I2:ф* R = 2 * 222 * 10 = 9680 Вт = 9,68 кВт. Векторная диаграмма напряжений и токов приведена на рис. 3.19

3.4. Активная, реактивная, комплексная и полная мощности трехфазной симметричной системы

Активной мощностью (часто просто мощностью) трехфазной системы называется сумма активных мощностей всех фаз источника энергии, равная сумме активных мощностей всех фаз приемника.

В симметричной трехфазной системе, т.е. в системе с симметричными генератором и приемником, при любой схеме их соединений для каждой фазы мощности источника энергии и приемника одинаковые. В этом случае Р = 3Р_ф и для каждой из фаз справедлива формула активной мощности синусоидального тока (2.55):

где j — угол сдвига фаз между фазными напряжением и током.

Заменив действующие значения фазных тока и напряжения линейными при соединении фаз источника энергии и приемника звездой [см. (3.8), (3.9)] и треугольником [см. (3.14), (3.15)], получим одно и то же выражение для активной мощности симметричной трехфазной системы:

В промышленных установках приемники обычно симметричные или почти симметричные, т. е. мощность может быть вычислена по (3.16).

В общем случае реактивной мощностью трехфазной системы называется сумма реактивных мощностей всех фаз источника энергии, равная сумме реактивных мощностей всех фаз приемника. Реактивная мощность симметричной трехфазной системы по (2.58)

Q_ф = 3Q_ф = 3U_фIsinj,

или после замены действующих значений фазных тока и напряжения линейными

Комплексной мощностью трехфазной системы называется сумма комплексных мощностей всех фаз источника энергии, равная сумме комплексных мощностей всех фаз приемника.

Полная мощность симметричной трехфазной системы

3.5. Сравнение условий работы приемника при соединениях его фаз треугольником и звездой

Схема соединения трех фаз приемника не зависит от схемы соединения трех фаз генератора. Соединение фаз приемника треугольником часто переключается на соединение звездой для изменения тока и мощности, например для уменьшения пусковых токов трехфазных двигателей, изменения температуры трехфазных электрических печей и т. д.

Рассмотрим, как изменяются действующие значения токов симметричного приемника с полным фазным сопротивлением z_ф при переключении фаз со звезды на треугольник, например, простым трехполюсным переключателем (рис. 3.10).

При соединении фаз приемника звездой между действующими значениями фазных и линейных токов (3.9) и напряжений (3.8) справедливы соотношения

из которых следует, что

При соединении фаз приемника треугольником между действующими значениями фазных и линейных токов (3.14) и напряжений (3.15) справедливы соотношения

из которых следует, что

Сопоставив выражения для действующих значений линейных токов при соединении фаз приемника звездой (3.19) и треугольником (3.20), получим при одном и том же действующем значении линейного напряжения U_л и одинаковых полных фазных сопротивлениях z_ф

I_лD = 3I_лY, а для действующих значений фазных токов

Активная мощность трехфазного симметричного приемника при любой из схем соединения по (3.16) равна

Вследствие уменьшения действующего значения линейного тока при переключении фаз приемника с треугольника на звезду мощность уменьшается в 3 раза, т. е.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

Способы вычислений мощности трехфазной цепи

Вычисление величины полной мощности. Расчет полной мощности электрической цепи требует знания ее активной и реактивной составляющих, соотношение которых в любой схеме описывается треугольником мощностей.

Для вычисления активной (Р) и реактивной (Q) составляющих 3-х фазной цепи проводится суммирование их величин в каждой фазе по формулам:

I_A, I_В, I_С, U_A, U_В, U_С – вектора токов и напряжений в фазах, Φ – угол сдвига фаз векторов тока относительно напряжения.

Для симметричного режима работы схемы во всех фазах выполняется равенство мощностей. Поэтому общую величину мощности можно получить простым умножением фазной составляющей на количество фаз в системе:

Делаем замену фазных составляющих линейными по их соотношениям для схемы звезды: I_Л=I_Ф, U_Ф=U_Л/√3.

В результате получаем:

Заменяем фазные составляющие линейными для схемы треугольника по их соотношениям: I_Ф=I_Л/√3, U_Ф=U_Л.

Таким образом, получилось, что зависимость от вариантов соединения элементов цепи схемой γ либо Δ в 3-х фазной симметричной системе значения мощностей отсутствует. Они вычисляются по одним и тем же формулам:

Р=√3∙U∙I∙cosφ [Вт]; Q=√3∙U∙I∙sinφ [вар]; S=√(Р 2 +Q 2 ) [ВА].

Для данных выражений сложилось правило: подставлять линейные значения векторов U и I без указания их линейных индексов.

Способы измерений мощности В энергетике существует постоянная необходимость измерения электрических величин. Активная составляющая полной мощности замеряется ваттметром, а реактивная – варметром. Ваттметр работает по алгоритму, описанному формулой:

U_W, I_W – те вектора, которые подвели к клеммам прибору для замера активной составляющей.

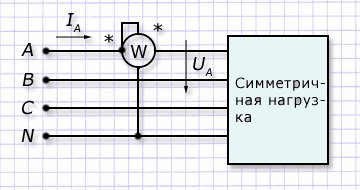Практика электрических измерений предлагает несколько вариантов подключения к электросети ваттметров. Они выбираются в зависимости от схемы выполненный коммутации нагрузок и ее характеристик.

В симметричной 3-х фазной системе достаточно включить один ваттметр в любую фазу для постоянного замера активной мощности с последующим утроением полученного результата по алгоритму Р=3W=3U_Ф∙I_Ф∙cosφ.

Однако, этот простой способ только ориентировочно оценивает замеряемые величины, имеет большие погрешности. Поэтому, он малоприемлем для выполнения замеров, требующих высокой точности и в решении коммерческих задач.

Более точные замеры активной составляющей для звезды с нейтральным проводом обеспечивает использование в измерении трех ваттметров.

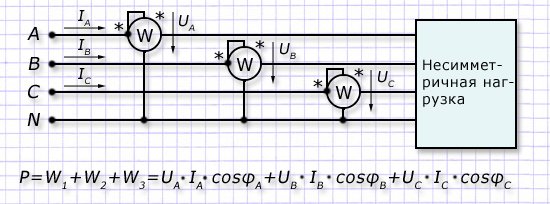
Выполняемые отдельно в каждой фазе измерения обладают большей точностью. Сложение показателей всех трех ваттметров предоставляет информацию об активной мощности с минимальными погрешностями.

При несимметричной нагрузке в 3-х фазной сети без нейтрального провода применяется способ замера двумя ваттметрами.

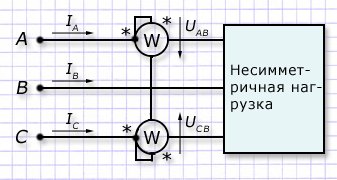
Особенность замера состоит в том, что линейные/фазные токи в такой электрической цепи взаимосвязаны 1-м законом Кирхгофа, когда их сумма I_А+I_В+I_С=0. Если математически сложить показания обоих ваттметров и описать их математическими методами, то получим выражения:

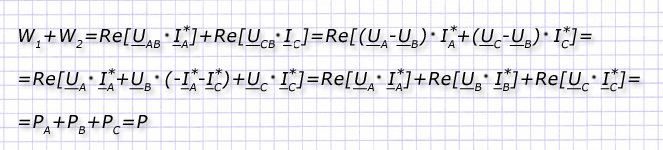
В итоге, подтвердилось предположение, что два ваттметра замеряют активную мощность данной схемы при суммировании их показаний. На показания любого из них влияют характеристики и величины нагрузок.

Вид векторов напряжений и токов на комплексной плоскости для симметричной нагрузки демонстрирует диаграмма:

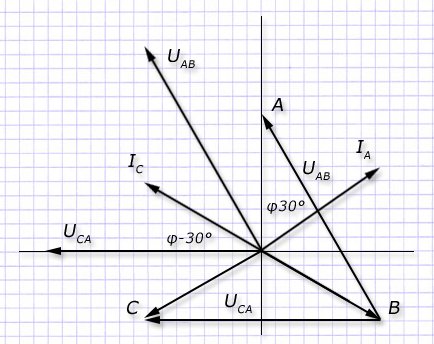
Из которой понятно, что для обеспечения показаний ваттметров используются выражения:

По результатам анализа данных формул достаточно несложно сделать следующие выводы:

1. При φ=0 создается равенство показаний обоих ваттметров, что весьма характерно для чистой активной нагрузки;

2. Когда 0≤φ≤90° (четверть активно-индуктивной нагрузки квадранта) показания 2-го ваттметра больше, чем первого (W2>W1). В этом же квадранте все показания у 1-го ваттметра приобретают отрицательную величину при значениях φ>60°;

3. В случае 0≥φ≥90° (четверть активно-емкостной нагрузки квадранта) показания 1-го ваттметра больше, чем второго (W1>W2). В этом же квадранте показания 2-го ваттметра приобретают отрицательную величину при значениях φ

Мощность трехфазной сети

В цепи постоянного тока мощность определяется довольно просто – это произведение тока и напряжения. Они не изменяются во времени и есть постоянной величиной, соответственно и мощность является постоянной, то есть система уравновешена.

С сетями переменного напряжения все гораздо сложнее. Они бывают однофазные, двухфазные, трехфазные и т.д. Наибольшее распространение получили однофазные и трехфазные сети в силу своего удобства и наименьших затрат.

Рассмотрим трехфазную систему питания

Такие цепи, могут соединяться в звезду или в треугольник. Для удобства чтение схем и во избежание ошибок фазы принято обозначать U, V, W или А, В, С.

Схема соединения звезда:

Схема соединения фаз в звезду

Для соединения звездой суммарное напряжение в точке N равно нулю. Мощность трехфазного тока в данном случае тоже будет постоянной величиной, в отличии от однофазного. Это значит что трехфазная система уравновешена, в отличии от однофазной, то есть мощность трехфазной сети постоянна. Мгновенно значение полной трехфазной мощности будет равно:

В данном типе соединения присутствуют два вида напряжения – фазное и линейное. Фазное – это напряжение между фазой и нулевой точкой N:

Фазное напряжение в цепи

Линейное – между фазами:

Линейное напряжение

Поэтому полная мощность трехфазной сети для такого типа соединения будет равна:

Но поскольку линейное и фазное напряжение отличаются между собой в , но считается сумма фазовых мощностей. При расчете трехфазных цепей такого типа принято пользоваться формулой:

Соответственно для активной:

Для реактивной:

Схема соединения в треугольник

Как видим при таком виде соединения, фазное и линейное напряжение равны, из чего следует, что мощность для соединения в треугольник равна:

Измерение мощности

Измерение активной мощности в сетях производится с помощью ваттметра

Цифровой ваттметр Аналоговый ваттметр

В зависимости от схемы соединения нагрузки и его характера (симметричная или несимметричная) схемы подключения приборов могут разниться. Рассмотрим случай с симметричной нагрузкой:

Схема включения ваттметра при симметричной нагрузке

Здесь измерение проводится всего лишь в одной фазе и далее согласно формуле умножается на три. Этот способ позволяет сэкономить на приборах и уменьшить габариты измерительной установки. Применяется, когда не нужна большая точность измерения в каждой фазе.

Измерение при несимметричной нагрузке:

Схема включения ваттметра при несимметричной нагрузке

Этот способ более точный, так как позволяет измерить мощность каждой фазы, но это требует трех приборов, больших габаритных размеров установки и обработки показаний с трех приборов.

Измерении в цепи без нулевого проводника:

Схема включения ваттметра при отсутствии нулевого провода

Эта схема требует двух приборов. Этот способ основывается на первом законе Кирхгофа

I_A+I_B+I_C=0. Из этого следует, что сумма показаний двух ваттметров равна трехфазной мощности этой цепи. Ниже показана векторная диаграмма для данного случая:

Векторная диаграмма включения двух ваттметров при различных видах нагрузки

Мы можем сделать вывод, что показания приборов зависят не только от величины, но еще и от характера нагрузки.

Из диаграммы следует, что мы можем определить показание приборов аналитически:

Проанализировав полученный результат можем сделать вывод что, при преобладании активной нагрузки (φ=0) результаты измерения ваттметров тождественны (W₁=W₂). При активной и индуктивной (R-L) показания W₁ меньше чем W₂ (W₁ 60 0 показания W₁ вообще отрицательные (W₁ W₂, а при φ 0 показания W₂ Новый стандарт многосвязной сети с Bluetooth

• Солнечное затмение испытывает надежность электрической сети
• Устройство контактора с управлением от сети постоянного тока
• Мощность периодических несинусоидальных токов
• Перевод энергосистемы на постоянный ток может…

Комментарии к статье “ Мощность трехфазной сети ”

В формуле мощности при соединении треугольником надо дописать что Iф= КОРЕНЬ из I ЛИНЕЙНОГО, а значит окончательнаяф формула принимает вид почти ТАКОЙ ЖЕ как и для мощности при соединении звездой — Р=КОРЕНЬ из ТРЁХ * Uфазное * I линейное*соs f

При чём U фазное = U линейное. То есть в обеих случаях формула мощности одна и та же.

ПОдскажите , клещами на проводниках 3 полючного автомата померили ток, получили значения. Как считать мощность через. корень квадратный? или как для однофазки P=UI

Все зависит от того, какую мощность вы хотите посчитать. Если полную, то да, S = UI. Для других мощностей нужно использовать другие формулы.

Добавить комментарий Отменить ответ

• Автоматизация технологических процессов (159)
• Альтернативная энергетика (32)
• Интернет вещей (IoT) (116)
• Микроконтроллеры (31)
• Моделирование электромеханических систем (22)
• Новости партнеров (1)
• Новости электроники (202)
• Основы электричества (33)
• Реактивная мощность (13)
• Робототехника (45)
• Станки с ЧПУ (43)
• Схемотехника (115)
• Теория автоматического управления (16)
• Электрика в быту (61)
• Электрические машины и аппараты. Трансформаторы (76)
• Электропривод (124)
• Электроснабжение (84)
• Электротехника (125)
• Энергосбережение (96)

• Магнитные пускатели — 114 184
• Логические элементы и их схемная реализация — 90 064
• Что такое активная, реактивная и полная мощность — 82 353
• В чем разница между NPN и PNP транзисторами? — 73 818
• Соотношение между фазными и линейными напряжениями. Номинальные напряжения — 70 161
• Ввод и распределение электроэнергии в многоквартирном доме — 67 229
• Что такое категории надежности электроснабжения? — 66 580
• Механические характеристики при торможении синхронных машин — 60 288
• Мощность трехфазной сети — 58 464
• Подключение амперметров к сети — 58 298

Дальше к плану следующей лекции
Обратно к плану данной лекции

Мощность трехфазного тока

§ 64. МОЩНОСТЬ ТРЕХФАЗНОГО ТОКА

Мощность, потребляемая нагрузкой от сети трехфазного тока, равна сумме мощностей, потребляемых отдельными фазами, т. е.

При равномерной нагрузке мощность, потребляемая каждой фазой,

где Uф — фазное напряжение,

cos j — коэффициент мощности нагрузки.

Мощность, потребляемая всеми тремя фазами,

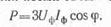
При соединении приемников энергии звездой соотношение меж­ду линейными и фазными значениями напряжений и токов:

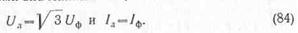
Следовательно, мощность, потребляемая нагрузкой от трехфазной

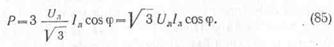
При соединении приемников энергии треугольником соотношение между линейными и фазными значениями напряжений и токов:

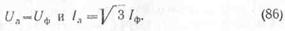
Следовательно, мощность, потребляемая нагрузкой,

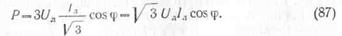
Таким образом, при равномерной нагрузке мощность, потребляе­мая от трехфазной сети, независимо от схемы включения нагрузки, выражается следующей формулой:

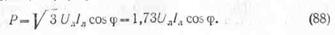
Пример. Линейное напряжение трехфазной осветительной установки равно 220 в, а линейный ток 9,9 а. Определить, сколько ламп включено параллельно в каждую фазу нагрузки при соединении этих фаз треугольником и какова мощность всей установки, если каждая лампа потребляет ток 0,52 a .

Решение. Фазное напряжение равно линейному, т. е

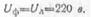
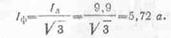
Число ламп, включенных параллельно в каждой фазе,

,

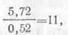
т. е. всего включено ламп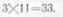

Мощность всей установки, имея в виду, что при осветительной нагрузке cos j=1, находим по следующей формуле:

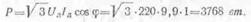
При неравномерной нагрузке мощности в фазах различный (P_A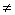P_B 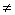P_C) и суммарная мощность, потребляемая нагрузкой, равна:

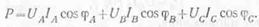
Для измерения мощности применяют специальные измерительные приборы, называемые ваттметрами. При симметричной нагрузке мощность, потребляемая от трехфазной системы, может быть определена одним однофазным ваттметром. В четырехпроводной системе (с нулевым проводом) токовая обмотка ваттметра включается последовательно в один из линейных проводов, а обмотка напряжения — между тем же линейным и нулевым проводами. При таком включении показание ваттметра определит мощность в одной фазе Рф, а так как при равномерной нагрузке мощности всех фаз одинаковы, то суммарная мощность трехфазной системы Р = 3 Рф.

В трехпроводной системе обмотка напряжения ваттметра включена на линейное напряжение сети, а по токовой его обмотке протекает линейный ток. Поэтому мощность трехфазной системы в 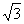раз больше показания ваттметра P_ω, т. е. Р=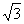Рω.

При несимметричной нагрузке одного ваттметра для определений мощности трехфазной системы недостаточно.

В четырехпроводной системе при несимметричной нагрузке необходимо включение трех ваттметров, обмотки напряжений которых включаются между нулевым и соответствующим линейным проводом. Каждый ваттметр измеряет мощность одной фазы и суммар­ная мощность трехфазной системы равна сумме показаний трех ваттметров, т. е. Р = Р₁ + Р₂ + Р₃.

В трехпроводной системе при несимметричной нагрузке наиболее часто используют схему двух ваттметров, которая не может быть использована в четырехпроводной системе. В схеме двух ваттметров обмотки напряжений каждого ваттметра соединены с входным зажимом обмотки тока и линейным проводом, оставшимся свободным. Полная мощность трехфазной системы равна сумме показа­ний ваттметров, т. е. Р=Р₁+Р₂

В лабораторной практике для этой схемы измерения мощности применяют один ваттметр и специальный переключатель, который без разрыва цепи тока дает возможность включать этот ваттметр как в один, так и в другой линейный провод.

При больших углах сдвига фаз между напряжением и током по­казания одного из ваттметров могут оказаться отрицательными и для измерения мощности необходимо изменить направление тока в обмотке тока, переключив ее. В этом случае суммарная мощность равна разности показаний ваттметров, т. е. Р = Р₁ — Р₂.

Энергия в трехфазной системе измеряется как однофазными, так и трехфазными счетчиками электрической энергии. Включение одно­фазных счетчиков в трехфазную сеть подобно включению ваттмет­ров, описанному выше.

Трехфазные счетчики составляются из двух или трех однофаз­ных, размещенных в одном корпусе и имеющих общий счетный ме­ханизм, и называются соответственно двухэлементными и трехэле­ментными. В трехпроводной системе (без нулевого провода) при­меняют двухэлементные, а в четыре проводной системе (с нулевым проводом) —трехэлементные счетчики. Схема включения счетчика электрической энергии указывается на съемной крышке, которой закрывается панель зажимов.

Мощности трехфазной симметричной системы

В нормально функционирующей трехфазной сети линейные напряжения (напряжения между каждой парой фазных проводников) равны друг другу по величине и различаются между собой по фазе на 120 градусов. Соответственно и фазные напряжения (напряжения между каждым фазным проводником и нейтральным проводником) равны между собой по величине и имеют аналогичные различия по фазе.

Как следует из вышесказанного, углы сдвига фаз между данными напряжениями равны между собой. Это и называется «симметричная трехфазная система напряжений».

Если к такой сети подключить симметричную нагрузку, то есть такую трехфазную нагрузку, при которой токи каждой из фаз будут равны по величине и по фазе, то такая нагрузка создаст симметричную систему токов (с одинаковыми углами сдвига фаз между ними). Это возможно при условии, когда во всех трех фазах нагрузки имеются одинаковые реактивные и активные сопротивления, то есть Za = Zb = Zc.

Поэтому и фазные токи оказываются в данных условиях равными по величине и по углу сдвига фаз между ними. Примеры симметричных нагрузок: трехфазный асинхронный двигатель, три одинаковые лампы накаливания — каждая на своей фазе, симметрично нагруженный трехфазный трансформатор и т.д.

Рассмотрим векторную диаграмму токов симметричной трехфазной нагрузки. Здесь легко увидеть, что геометрическая сумма векторов трех фазных токов обращается в ноль. Это значит, что при симметричной нагрузке ток нейтрального проводника будет равен нулю, и практически надобность в его использовании отпадает.

Если же к этой трехфазной сети с симметричной системой напряжений подключить несимметричную нагрузку, то есть такую нагрузку, при которой комплексные сопротивления нагрузки в каждой фазе различны (Za ≠ Zb ≠ Zc), то нагрузка создаст систему токов, которые будут различаться между собой по величине и по направлению (по сравнению с диаграммой токов, характерной для симметричной нагрузки). Значения этих фазных токов можно найти по закону Ома.

И тогда геометрическая сумма токов не обратится в ноль, а значит и в нейтральном проводнике будет иметь место переменный ток, поэтому нейтральный проводник в данном случае необходим. Примеры несимметричных нагрузок: лампы накаливания разной мощности в трех фазах, несимметрично нагруженный трехфазный трансформатор, нагрузки с разными коэффициентами мощности в трех фазах и т. д.

Нейтральный провод в данном случае обеспечит сохранение симметрии фазных напряжений несмотря на то, что нагрузка несимметрична. Вот почему четырехпроводная сеть допускает включение однофазных потребителей различной мощности и характера импеданса в разные фазы. Цепь каждой нагруженной фазы будет находится под фазным напряжением генератора независимо от разницы нагрузок между фазами.

Здесь изображена векторная диаграмма несимметричной нагрузки. На диаграмме легко видеть, что за счет наличия нулевого провода, ток в нем представляет собой геометрическую сумму векторов токов каждой из фаз, при этом фазные напряжения не испытывают перекоса, который непременно бы возник если бы нулевого провода при несимметричной нагрузке не было.

Если по какой-нибудь причине нейтральный провод оборвется во время питания несимметричной нагрузки, то возникнет резкий перекос напряжений и токов трехфазной сети, который может привести к аварии.

Перекос случится в этом случае потому, что три цепи нагрузки, питаемые трехфазным источником, вместе со внутренним сопротивлением источника, образуют три цепи разного импеданса, падение напряжения на каждой из которых будет разным и система напряжений трехфазной сети перестанет поэтому быть симметричной.

Ранее ЭлектроВести писали, что в озложение спецобязательств по компенсации низких цен на электроэнергию для населения через включение в тариф ГП «НЭК« Укрэнерго» на передачу (вместо тарифа на диспетчеризацию) приведет к тому, что дополнительная финансовая нагрузка будет перераспределена между потребителями, а не производителями электроэнергии.

ОСНОВЫ МЕТРОЛОГИИ И ЭЛЕКТРИЧЕСКИЕ ИЗМЕРЕНИЯ

КОНТРОЛЬНАЯ РАБОТА №1

ЗАДАЧА №5

ИЗМЕРЕНИЕ АКТИВНОЙ МОЩНОСТИ В ЦЕПЯХ ТРЕХФАЗНОГО ТОКА

Для измерения активной мощности трехпроводной цепи трехфазного тока с симметричной активно-индуктивной нагрузкой, соединенной звездой или треугольником, необходимо выбрать два одинаковых ваттметра с номинальным током I _н , номинальным напряжением U _н и числом делений шкалы α_н = 150 дел.

Исходные данные для решения задачи приведены в табл.8

Таблица 8

Числовые значения для задачи №5

Предпоследняя цифра шифра

Мощность цепи S

Коэффициент мощности cos φ

Фазное напряжение U _ф

Последовательные обмотки ваттметров включены в провода

1. По данным варианта для нормального режима работы цепи:

а) начертить схему включения ваттметров в цепь;

б) доказать, что активную мощность трехпроводной цепи трехфазного тока можно представить в виде суммы двух слагаемых;

в) построить в масштабе векторную диаграмму, выделив на ней векторы напряжений и токов, под действием которых находятся параллельные и последовательные обмотки ваттметров;

г) определить мощности Р₁ и Р₂, измеряемые каждым из ваттметров;

д) определить число делений шкалы α₁ и α₂, на которые отклоняются стрелки ваттметров.

1. По данным варианта при обрыве одной фазы приемника энергии:

а) начертить схему включения ваттметров в цепь;

б) п остроить в масштабе векторную диаграмму, выделив на ней векторы напряжений и токов, под действием которых находятся параллельные и последовательные обмотки ваттметров;

в) определить мощности Р₁ и Р₂, измеряемые каждым из ваттметров;

г) определить число делений шкалы α₁ и α₂, на которые отклоняются стрелки ваттметров.

Результаты расчетов записать в табл. 9.

1. а) Схема включения ваттметров показана на рис. 1.

1. б) Мгновенная мощность трехфазной цепи может быть выражена как сумма мощностей отдельных фаз:

Для нулевой точки приемников энергии, соединенных звездой (рис. 1), по первому закону Кирхгофа

,

откуда каждый из линейных токов можно выразить через два других:

Подставив одно из этих выражений, например для тока i_B , в формулу (1), получим:

Следовательно, мгновенную мощность трехфазной цепи можно представить суммой двух слагаемых, первое из которых и второе

Переходя от мгновенной мощности к средней (активной) и допуская, что токи и напряжения синусоидальны, получаем:

где φ₁ – угол сдвига фаз между током I_A и линейным напряжением U_AB

φ₁ –между током I_C и линейным напряжением U_CB .

Первое слагаемое P ’ можно измерить одним ваттметром, а второе P ’’- вторым, если ваттметры соединены следующим образом: токовая цепь первого ваттметра в соответствии с индексом А у тока I_A включается в рассечку провода А, и т.к. ток положителен, то генераторный зажим ее соединяется с источником питания (рис.1). Генераторный зажим параллельной цепи в соответствии с первой частью индекса А у напряжения U_AB соединен с проводом А, а не генераторный зажим той же цепи в соответствии со второй частью индекса B присоединен к проводу B . Аналогично включается второй ваттметр. Активная мощность трехфазной цепи равна алгебраической сумме показаний двух ваттметров.

1. в) В частном случае при симметричной системе напряжений и одинаковой нагрузке фаз ψ₁ = 30 – φ и ψ₁ = 30 + φ и показания ваттметров будут

Полная мощность трехфазной цепи . Отсюда находим линейный ток

Линейное напряжение найдем, зная фазное

Векторная диаграмма построена на рис. 2.

1. г) Определим мощности, измеряемые ваттметрами:

1. д) Выбираем ваттметры с номинальным током I _н = 10 А и номинальным напряжением U _н = 300 В, числом делений шкалы α_н = 150 дел.

Тогда отклонения стрелок ваттметров будут равны:

1. Схема включения ваттметров при обрыве фазы B показана на рис. 3

2. б) Векторная диаграмма при обрыве фазы B построена на рис. 4.

2. в) При обрыве фазы С ток в ней равен нулю. Две другие фазы соединены последовательно и включены на линейное напряжение U_АВ. Сопротивление фазы В при нормальном режиме работы

Для симметричной трехфазной системы ток в последовательно соединенных фазах определяется как

1. г) Число делений первого ваттметра и число делений второго ваттметра

Онлайн журнал электрика

Статьи по электроремонту и электромонтажу

• Справочник электрика
  • Бытовые электроприборы
  • Библиотека электрика
  • Инструмент электрика
  • Квалификационные характеристики
  • Книги электрика
  • Полезные советы электрику
  • Электричество для чайников
• Справочник электромонтажника
  • КИП и А
  • Полезная информация
  • Полезные советы
  • Пусконаладочные работы
• Основы электротехники
  • Провода и кабели
  • Программа профессионального обучения
  • Ремонт в доме
  • Экономия электроэнергии
  • Учёт электроэнергии
  • Электрика на производстве
• Ремонт электрооборудования
  • Трансформаторы и электрические машины
  • Уроки электротехники
  • Электрические аппараты
  • Эксплуатация электрооборудования
• Электромонтажные работы
  • Электрические схемы
  • Электрические измерения
  • Электрическое освещение
  • Электробезопасность
  • Электроснабжение
  • Электротехнические материалы
  • Электротехнические устройства
  • Электротехнологические установки

Активная, реактивная и полная мощности трехфазной симметричной системы

Активная и реактивная и полная мощности трехфазной симметричной системы

Активной мощностью (нередко просто мощностью) трехфазной си­стемы именуется сумма активных мощностей всех фаз источника энер­гии, равная сумме активных мощностей всех фаз приемника. В симметричной трехфазной системе, т. е. системе с симметричными генератором и приемником, при хоть какой схеме их соединений для ка­ждой фазы мощности источника энергии и приемника однообразные. В данном случае Р= 3Рф и для каждой из фаз справедлива формула активной мощности синусоидального тока Рф = UфIф cos? где ? – угол сдвига фаз меж фазными напряжениеми током.

Заменив действующие значения фазных тока и напряжения линей­ными при соединении источника энергии и приемника по схеме звезда и треугольник, получим одно и то же выраже­ние для активной мощности симметричной трехфазной системы:

Р =3UфIф cos?=v3U_лI_лcos?

В промышленных установках приемники обычно симметричные либо практически симметричные, т. е. мощность может быть вычислена по приведенной выше формуле.

Трехфазные счетчики активной и реактивной энергии

В общем случае реактивной мощностью трехфазной системы назы­вается сумма реактивных мощностей всех фаз источника энергии, рав­ная сумме реактивных мощностей всех фаз приемника. Реактивная мощность симметричной трехфазной системы

Q = 3Qф = 3UфIфsin?

либо после подмены действующих значений фазных тока и напряжения линейными

Q = v3U_лI_лsin?

Всеохватывающей мощностью трехфазной системы именуется сумма всеохватывающих мощностей всех фаз источника энергии, равная сумме всеохватывающих мощностей всех фаз приемника.

Полная мощность симметричной трехфазной системы S=v3U_лI_л