Что гласит закон Кулона?

Закон Кулона и его применение в электротехнике

Так же как в ньютоновой механике гравитационное взаимодействие всегда имеет место между телами обладающими массами, аналогичным образом в электродинамике электрическое взаимодействие свойственно телам, обладающим электрическими зарядами. Обозначается электрический заряд символом «q» или «Q».

Можно даже сказать, что понятие электрического заряда q в электродинамике чем-то схоже с понятием гравитационной массы m в механике. Но в отличие от гравитационной массы, электрический заряд характеризует свойство тел и частиц вступать в силовые электромагнитные взаимодействия, и эти взаимодействия, как вы понимаете, не являются гравитационными.

Человеческий опыт исследования электрических явлений содержит множество экспериментальных результатов, и все эти факты позволили физикам прийти к следующим однозначным выводам относительно электрических зарядов:

1. Электрические заряды бывают двух родов — условно их можно разделить на положительные и отрицательные.

2. От одного заряженного предмета к другому электрические заряды можно передавать: допустим, путем соприкосновения тел друг с другом — заряд между ними можно разделить. При этом электрический заряд вовсе не является обязательной составной частью тела: в различных условиях один и тот же предмет может обладать разным по величине и по знаку зарядом, либо заряд может отсутствовать. Таким образом, заряд не является чем-то неотъемлемым для носителя, и в то же самое время заряд не может существовать без носителя заряда.

3. В то время как гравитирующие тела всегда притягиваются друг к другу, электрические заряды могут как взаимно притягиваться, так и взаимно отталкиваться. Разноименные заряды взаимно притягиваются, одноименные — друг от друга отталкиваются.

Закон сохранения электрического заряда — фундаментальный закон природы, он звучит так: «алгебраическая сумма зарядов всех тел внутри изолированной системы остается постоянной». Это значит, что внутри замкнутой системы невозможно появление или исчезновение зарядов лишь одного знака.

Сегодня научная точка зрения такова, что изначально носители заряда — это элементарные частицы. Элементарные частицы нейтроны (электрически нейтральные), протоны (положительно заряженные) и электроны (заряженные отрицательно) образуют атомы.

Из протонов и нейтронов состоят ядра атомов, а электроны образуют оболочки атомов. Модули зарядов электрона и протона равны по величине элементарному заряду е, но по знаку заряды этих частиц противоположны между собой.

Взаимодействие электрических зарядов — Закон Кулона

Что касается непосредственно взаимодействия электрических зарядов друг с другом, то в 1785 году французский физик Шарль Кулон экспериментально установил и описал этот основной закон электростатики, фундаментальный закон природы, ни из каких других законов не вытекающий. Ученый в своей работе изучал взаимодействие неподвижных точечных заряженных тел, и измерял силы их взаимного отталкивания и притяжения.

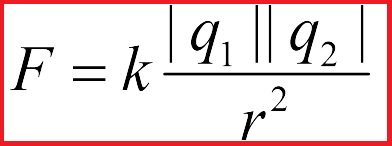
Кулон экспериментально установил следующее: «Силы взаимодействия неподвижных зарядов прямо пропорциональны произведению модулей и обратно пропорциональны квадрату расстояния между ними».

Это и есть формулировка Закона Кулона. И хотя точечных зарядов в природе не существует, только применительно к точечным зарядам и можно говорить о расстоянии между ними, в рамках данной формулировки Закона Кулона.

На самом же деле, если расстояния между телами сильно превосходят их размеры, то ни размер, ни форма заряженных тел, особо не повлияют на их взаимодействие, а значит тела для данной задачи справедливо можно будет считать точечными.

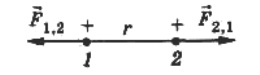
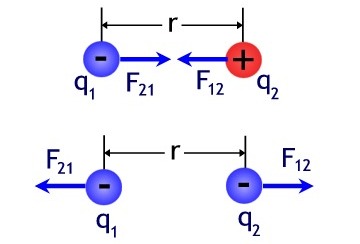
Рассмотрим такой пример. Подвесим на нитках пару заряженных шаров. Поскольку они как-то заряжены, то станут либо отталкиваться друг от друга, либо притягиваться друг к другу. Так как силы направлены вдоль прямой, соединяющей данные тела, — силы эти центральные.

Для обозначения сил, действующих со стороны каждого из зарядов на другой, запишем: F12 – сила действия второго заряда на первый, F21 – сила действия первого заряда на второй, r12 – радиус-вектор от второго точечного заряда к первому. Если заряды имеют одинаковый знак, то сила F12 будет сонаправлена радиусу-вектору, если же у зарядов разные знаки — F12 будет направлена противоположно радиусу-вектору.

При помощи закона взаимодействия точечных зарядов (Закона Кулона) можно теперь находить силу взаимодействия для любых точечных зарядов или точечных заряженных тел. Если же тела не точечные, то их мысленно разбивают на мелке элементы, каждый из которых можно было бы принять за точечный заряд.

После нахождения сил, действующих между всеми мелкими элементами, силы эти геометрически складывают, — находят результирующую силу. Элементарные частицы тоже взаимодействуют друг с другом согласно Закону Кулона, и по сей день не замечено никаких нарушений этого фундаментального закона электростатики.

Применение Закона Кулона в электротехнике

В современной электротехнике нет области, где в том или ином виде не работал бы Закон Кулона. Начиная с электрического тока, заканчивая просто заряженным конденсатором. Особенно те области, которые касаются электростатики, — они на 100% связаны с Законом Кулона. Рассмотрим только несколько примеров.

Простейший случай — введение диэлектрика. Сила взаимодействия зарядов в вакууме всегда больше силы взаимодействия тех же зарядов в условиях, когда между ними расположен какой-то диэлектрик.

Диэлектрическая проницаемость среды — это как раз та величина, которая позволяет количественно определить значения сил, независимо от расстояния между зарядами и от их величин. Достаточно силу взаимодействия зарядов в вакууме разделить на диэлектрическую проницаемость внесенного диэлектрика — получим силу взаимодействия в присутствии диэлектрика.

Сложное исследовательское оборудование — ускоритель заряженных частиц. Базируется работа ускорителей заряженных частиц на явлении взаимодействия электрического поля и заряженных частиц. Электрическое поле совершает в ускорителе работу увеличивая энергию частицы.

Если рассмотреть здесь ускоряемую частицу как точечный заряд, а действие ускоряющего электрического поля ускорителя — как суммарную силу со стороны других точечных зарядов, то и в этом случае полностью соблюдается Закон Кулона. Магнитное поле лишь направляет частицу силой Лоренца, но не изменяет её энергии, только задаёт траекторию для движения частиц в ускорителе.

Защитные электротехнические сооружения. Важные электроустановки всегда оснащаются такой простой на первый взгляд вещью, как молниеотвод. А молниеотвод в своей работе тоже не обходится без соблюдения Закона Кулона. Во время грозы на Земле появляются большие индуцированные заряды — согласно Закону Кулона притягиваются в направлении грозового облака. На поверхности Земли возникает в результате сильное электрическое поле.

Напряжённость этого поля особенно велика возле острых проводников, и поэтому на заостренном конце молниеприемника зажигается коронный разряд — заряд из Земли стремится, повинуясь Закону Кулона, притянуться к противоположному заряду грозового облака.

Воздух вблизи молниеотвода в результате коронного разряда сильно ионизируется. Вследствие этого напряжённость электрического поля вблизи острия уменьшается (как и внутри любого проводника), индуцированные заряды не могут накапливаться на здании и вероятность возникновения молнии снижается. Если же молния, так случится, ударит в молниеотвод, то заряд просто уйдет в Землю, не повредит установку.

Закон Кулона и единица измерения электрического заряда

Закон Кулона очень напоминает закон всемирного тяготения, только применимо к зарядам, а не к массам тел. Открыт он был экспериментально в 1785 году французским ученым Шарлем Кулоном.

Позднее он получил блестящее экспериментальное подтверждение. Для формулирования закона Кулона вначале надо ввести такое понятие как «точечный заряд».

Введение понятия «точечный заряд»

Точечными зарядами можно считать заряженные тела, в случае, когда их форма и размеры не оказывают сколько-нибудь существенного влияния на взаимодействие между этими телами.

Такое возможно, когда речь идет о телах, удаленных друг от друга на расстояния, много большие их размеров. Также следует учитывать, что закон Кулона применим в случае, когда среда, в которую помещены оба тела вакуум.

В случае, когда мы имеем воздух вместо вакуума, можно приближенно считать закон Кулона выполняющимся, так как воздух оказывает очень малое влияние на силу взаимодействия точечных зарядов.

Формулировка закона Кулона

Итак, закон Кулона гласит: сила взаимодействия двух точечных зарядов в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.

Можно записать закон Кулона в виде формулы:

F=k |q_1 ||q_2 | / r^2,

где |q_1 | и |q_2 | модули зарядов,

r расстояние между зарядами,

k коэффициент пропорциональности, зависящий от принятой системы единиц, численно он равен силе взаимодействия единичных зарядов на расстоянии, принятом за единицу длины.

Силу взаимодействия между точечными зарядами называют кулоновской.

Формула закона Кулона имеет тот же вид, что и закон всемирного тяготения, только вместо масс стоят модули зарядов, а вместо гравитационной постоянной коэффициент пропорциональности.

Стоит также отметить, что, как и в случае с законом тяготения, кулоновские силы действуют вдоль прямой, соединяющей эти заряды.

Единица измерения заряда — Кулон

За единицу заряда приняли кулон (1 Кл) в честь Шарля Кулона. Так как существует известная величина единичного элементарного заряда заряда электрона (протона), то можно было принять величину заряда, равной ей.

Но это слишком маленькая величина, и она не подходит для многих бытовых и промышленных расчетов, так как расчеты могли бы стать слишком громоздкими и неудобными. Такая величина принята и пригодна в ядерной физике.

Для классической же физики требовалось ввести иную величину. Поэтому, исходя из уже известных и используемых величин, приняли величину заряда в 1 Кл, равную заряду, проходящему через поперечное сечение проводника за 1 с при силе тока в 1 А.

Заряд в 1 Кл очень большая величина. В случае, когда два точечных заряда обладают каждый таким зарядом, сила их взаимодействия будет примерно равна силе, с которой Земля притягивает груз весом в 1 т.

Поэтому придать такой заряд маленькому телу невозможно, так как по закону Кулона одноименные заряды будут отталкивать кулоновскими силами.

Однако в проводнике протекание такого заряда возможно. Например, через спираль лампочки мощностью 60 Вт за 1 с проходит заряд чуть меньший 1 Кл.

Поэтому всегда следует помнить, что электричество это не шутка, а мощная сила, и относиться с предосторожностями к электроприборам под напряжением.

Нужна помощь в учебе?

Все неприличные комментарии будут удаляться.

Закон Кулона простыми словами

• История открытия
• Формулировка
• Формула Кулона для диэлектрической среды
• Как направлены силы
• Применение на практике

История открытия

Ш.О. Кулон в 1785 г. впервые экспериментально доказал взаимодействия описанные законом. В своих опытах он использовал специальные крутильные весы. Однако еще в 1773 г. было доказано Кавендишем, на примере сферического конденсатора, что внутри сферы отсутствует электрическое поле. Это говорило о том, что электростатические силы изменяются в зависимости от расстояния между телами. Если быть точнее — квадрату расстояния. Тогда его исследования не были опубликованы. Исторически сложилось так, что это открытие было названо в честь Кулона, аналогичное название носит и величина, в которой измеряется заряд.

Формулировка

Определение закона Кулона гласит: В вакууме F взаимодействия двух заряженных тел прямо пропорционально произведению их модулей и обратно пропорционально квадрату расстояния между ними.

Звучит кратко, но может быть не всем понятно. Простыми словами: Чем больший заряд имеют тела и чем ближе они находятся друг к другу, тем больше сила.

И наоборот: Если увеличить расстояние межу зарядами — сила станет меньше.

Формула правила Кулона выглядит так:

Обозначение букв: q — величина заряда, r — расстояние межу ними, k — коэффициент, зависит от выбранной системы единиц.

Величина заряда q может быть условно-положительной или условно-отрицательной. Это деление весьма условно. При соприкосновении тел она может передаваться от одного к другому. Отсюда следует, что одно и то же тело может иметь разный по величине и знаку заряд. Точечным называется такой заряд или тело, размеры которого много меньше, чем расстояние возможного взаимодействия.

Стоит учитывать что среда, в которой расположены заряды, влияет на F взаимодействия. Так как в воздухе и в вакууме она почти равна, открытие Кулона применимо только для этих сред, это одно из условий применения этого вида формулы. Как уже было сказано, в системе СИ единица измерения заряда — Кулон, сокращено Кл. Она характеризует количество электричества в единицу времени. Является производной от основных единиц СИ.

Стоит отметить, что размерность 1 Кл избыточна. Из-за того что носители отталкиваются друг от друга их сложно удержать в небольшом теле, хотя сам по себе ток в 1А небольшой, если он протекает в проводнике. Например в той же лампе накаливания на 100 Вт течет ток в 0,5 А, а в электрообогревателе и больше 10 А. Такая сила (1 Кл) примерно равна действующей на тело массой 1 т со стороны земного шара.

Вы могли заметить, что формула практически такая же, как и в гравитационном взаимодействии, только если в ньютоновской механике фигурируют массы, то в электростатике — заряды.

Формула Кулона для диэлектрической среды

Коэффициент с учетом величин системы СИ определяется в Н 2 *м 2 /Кл 2 . Он равен:

Во многих учебниках этот коэффициент можно встретить в виде дроби:

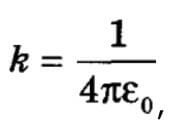
Здесь Е= 8,85*10-12 Кл2/Н*м2 — это электрическая постоянная. Для диэлектрика добавляется E — диэлектрическая проницаемость среды, тогда закон Кулона может применяться для расчетов сил взаимодействия зарядов для вакуума и среды.

С учетом влияния диэлектрика имеет вид:

Отсюда мы видим, что введение диэлектрика между телами снижает силу F.

Как направлены силы

Заряды взаимодействуют друг с другом в зависимости от их полярности — одинаковые отталкиваются, а разноименные (противоположные) притягиваются.

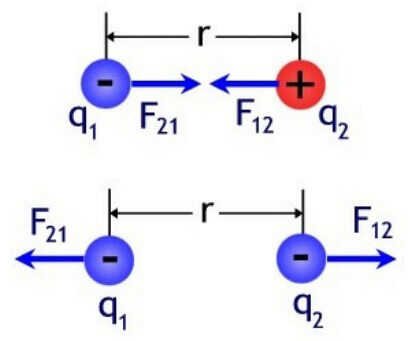
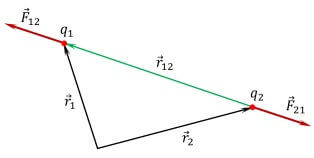
Кстати это главное отличие от подобного закона гравитационного взаимодействия, где тела всегда притягиваются. Силы направлены вдоль линии, проведенной между ними, называют радиус-вектором. В физике обозначают как r₁₂ и как радиус-вектор от первого ко второму заряду и наоборот. Силы направлены от центра заряда к противоположному заряду вдоль этой линии, если заряды противоположны, и в обратную сторону, если они одноименные (два положительных или два отрицательных). В векторном виде:

Сила, приложенная к первому заряду со стороны второго обозначается как F_12. Тогда в векторной форме закон Кулона выглядит следующим образом:

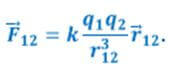
Для определения силы приложенной ко второму заряду используются обозначения F₂₁ и R₂₁.

Если тело имеет сложную форму и оно достаточно большое, что при заданном расстоянии не может считаться точечным, тогда его разбивают на маленькие участки и считают каждый участок как точечный заряд. После геометрического сложения всех получившихся векторов получают результирующую силу. Атомы и молекулы взаимодействуют друг с другом по этому же закону.

Применение на практике

Работы Кулона очень важны в электростатике, на практике они применяется в целом ряде изобретений и устройств. Ярким примером можно выделить молниеотвод. С его помощью защищают здания и электроустановки от грозы, предотвращая тем самым пожар и выход из строя оборудования. Когда идёт дождь с грозой на земле появляется индуцированный заряд большой величины, они притягиваются в сторону облака. Получается так, что на поверхности земли появляется большое электрическое поле. Возле острия молниеотвода оно имеет большую величину, в результате этого от острия зажигается коронный разряд (от земли, через молниеотвод к облаку). Заряд от земли притягивается к противоположному заряду облака, согласно закону Кулона. Воздух ионизируется, а напряженность электрического поля уменьшается вблизи конца молниеотвода. Таким образом, заряды не накапливаются на здании, в таком случае вероятность удара молнии мала. Если же удар в здание и произойдет, то через молниеотвод вся энергия уйдет в землю.

В серьезных научных исследованиях применяют величайшее сооружение 21 века – ускоритель частиц. В нём электрическое поле выполняет работу по увеличению энергии частицы. Рассматривая эти процессы с точки зрения воздействия на точечный заряд группой зарядов, тогда все соотношения закона оказываются справедливыми.

Напоследок рекомендуем просмотреть видео, на котором предоставлено подробное объяснение Закона Кулона:

Полезное по теме:

Закон Кулона, конденсатор, сила тока, закон Ома, закон Джоуля – Ленца

Теория к заданию 14 из ЕГЭ по физике

Закон Кулона

Закон Кулона — это один из основных законов электростатики. Он определяет величину и направление силы взаимодействия между двумя неподвижными точечными зарядами.

Под точечным зарядом понимают заряженное тело, размер которого много меньше расстояния его возможного воздействия на другие тела. В таком случае ни форма, ни размеры заряженных тел не влияют практически на взаимодействие между ними.

Закон Кулона экспериментально впервые был доказан приблизительно в 1773 г. Кавендишем, который использовал для этого сферический конденсатор. Он показал, что внутри заряженной сферы электрическое поле отсутствует. Это означало, что сила электростатического взаимодействия меняется обратно пропорционально квадрату расстояния, однако результаты Кавендиша не были опубликованы.

В 1785 г. закон был установлен Ш. О. Кулоном с помощью специальных крутильных весов.

Опыты Кулона позволили установить закон, поразительно напоминающий закон всемирного тяготения.

Сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна произведению модулей зарядов и обратно пропорциональна квадрату расстояния между ними.

В аналитическом виде закон Кулона имеет вид:

где $|q_1|$ и $|q_2|$ — модули зарядов; $r$ — расстояние между ними; $k$ — коэффициент пропорциональности, зависящий от выбора системы единиц. Сила взаимодействия направлена по прямой, соединяющей заряды, причем одноименные заряды отталкиваются, а разноименные — притягиваются.

Сила взаимодействия между зарядами зависит также от среды между заряженными телами.

В воздухе сила взаимодействия почти не отличается от таковой в вакууме. Закон Кулона выражает взаимодействие зарядов в вакууме.

Кулон — единица электрического заряда. Кулон (Кл) — единица СИ количества электричества (электрического заряда). Она является производной единицей и определяется через единицу силы тока 1 ампер (А), которая входит в число основных единиц СИ.

За единицу электрического заряда принимают заряд, проходящий через поперечное сечение проводника при силе тока $1$А за $1$с.

То есть $1$ Кл$= 1А·с$.

Заряд в $1$ Кл очень велик. Сила взаимодействия двух точечных зарядов по $1$ Кл каждый, расположенных на расстоянии $1$ км друг от друга, чуть меньше силы, с которой земной шар притягивает груз массой $1$ т. Сообщить такой заряд небольшому телу невозможно (отталкиваясь друг от друга, заряженные частицы не могут удержаться в теле). А вот в проводнике (который в целом электронейтрален) привести в движение такой заряд просто (ток в $1$ А вполне обычный ток, протекающий по проводам в наших квартирах).

Коэффициент $k$ в законе Кулона при его записи в СИ выражается в $Н · м^2$ / $Кл^2$. Его численное значение, определенное экспериментально по силе взаимодействия двух известных зарядов, находящихся на заданном расстоянии, составляет:

Часто его записывают в виде $k=<1>/<4πε_0>$, где $ε_0=8.85×10^<-12>Кл^2$/$H·м^2$ — электрическая постоянная.

Электрическая емкость конденсатора

Электроемкость

Электроемкостью проводника $С$ называют численную величину заряда, которую нужно сообщить проводнику, чтобы изменить его потенциал на единицу:

Емкость характеризует способность проводника накапливать заряд. Она зависит от формы проводника, его линейных размеров и свойств среды, окружающей проводник.

Единицей емкости в СИ является фарада ($Ф$) — емкость проводника, в котором изменение заряда на $1$ кулон меняет его потенциал на $1$ вольт.

Электрический конденсатор

Электрический конденсатор (от лат. condensare, буквально сгущать, уплотнять) — устройство, предназначенное для получения электрической емкости заданной величины, способное накапливать и отдавать (перераспределять) электрические заряды.

Конденсатор — это система из двух или нескольких равномерно заряженных проводников с равными по величине зарядами, разделенных слоем диэлектрика. Проводники называются обкладками конденсатора. Как правило, расстояние между обкладками, равное толщине диэлектрика, намного меньше размеров самих обкладок, так что поле в конденсаторе практически все сосредоточено между его обкладками. Если обкладки являются плоскими пластинами, поле между ними однородно. Электроемкость плоского конденсатора определяется по формуле:

где $q$ — заряд конденсатора, $U$ — напряжение между его обкладками, $S$ — площадь пластины, $d$ — расстояние между пластинами, $ε_<0>$ — электрическая постоянная, $ε$ — диэлектрическая проницаемость среды.

Под зарядом конденсатора понимают абсолютное значение заряда одной из пластин.

Энергия поля конденсатора

Энергия заряженного конденсатора выражается формулами

которые выводятся с учетом выражений для связи работы и напряжения и для емкости плоского конденсатора.

Энергия электрического поля. Объемная плотность энергии электрического поля (энергия поля в единице объема) напряженностью $Е$ выражается формулой:

где $ε$ — диэлектрическая проницаемость среды, $ε_0$ — электрическая постоянная.

Сила тока

Электрическим током называется упорядоченное (направленное) движение заряженных частиц.

Сила электрического тока — это величина ($I$), характеризующая упорядоченное движение электрических зарядов и численно равная количеству заряда $∆q$, протекающего через определенную поверхность $S$ (поперечное сечение проводника) за единицу времени:

Итак, чтобы найти силу тока $I$, надо электрический заряд $∆q$, прошедший через поперечное сечение проводника за время $∆t$, разделить на это время.

Сила тока зависит от заряда, переносимого каждой частицей, скорости их направленного движения и площади поперечного сечения проводника.

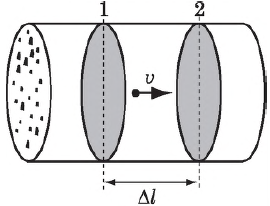
Рассмотрим проводник с площадью поперечного сечения $S$. Заряд каждой частицы $q_0$. В объеме проводника, ограниченном сечениями $1$ и $2$, содержится $nS∆l$ частиц, где $n$ — концентрация частиц. Их общий заряд $q=q_<0>nS∆l$. Если частицы движутся со средней скоростью $υ$, то за время $∆t=<�∆l>/<�υ>$ все частицы, заключенные в рассматриваемом объеме, пройдут через поперечное сечение $2$. Сила тока, следовательно, равна:

В СИ единица силы тока является основной и носит название ампер (А) в честь французского ученого А. М. Ампера (1755-1836).

Силу тока измеряют амперметром. Принцип устройства амперметра основан на магнитном действии тока.

Оценка скорости упорядоченного движения электронов в проводнике, проведенная по формуле для медного проводника с площадью поперечного сечения $1мм^2$, дает весьма незначительную величину — $∼0.1$ мм/с.

Закон Ома для участка цепи

Сила тока на участке цепи равна отношению напряжения на этом участке к его сопротивлению.

Закон Ома выражает связь между тремя величинами, характеризующими протекание электрического тока в цепи: силой тока $I$, напряжением $U$ и сопротивлением $R$.

Закон этот был установлен в 1827 г. немецким ученым Г. Омом и поэтому носит его имя. В приведенной формулировке он называется также законом Ома для участка цепи. Математически закон Ома записывается в виде следующей формулы:

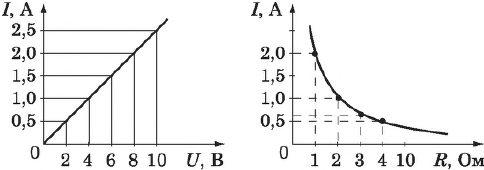
Зависимость силы тока от приложенной разности потенциалов на концах проводника называется вольт-амперной характеристикой (ВАХ) проводника.

Для любого проводника (твердого, жидкого или газообразного) существует своя ВАХ. Наиболее простой вид имеет вольт-амперная характеристика металлических проводников, заданная законом Ома $I=/$, и растворов электролитов. Знание ВАХ играет большую роль при изучении тока.

Закон Ома — это основа всей электротехники. Из закона Ома $I=/$ следует:

1. сила тока на участке цепи с постоянным сопротивлением пропорциональна напряжению на концах участка;
2. сила тока на участке цепи с неизменным напряжением обратно пропорциональна сопротивлению.

Эти зависимости легко проверить экспериментально. Полученные с использованием схемы, графики зависимости силы тока от напряжения при постоянном сопротивлении и силы тока от сопротивления представлены на рисунке. В первом случае использован источник тока с регулируемым выходным напряжением и постоянное сопротивление $R$, во втором — аккумулятор и переменное сопротивление (магазин сопротивлений).

Электрическое сопротивление

Электрическое сопротивление — это физическая величина, характеризующая противодействие проводника или электрической цепи электрическому току.

Электрическое сопротивление определяется как коэффициент пропорциональности $R$ между напряжением $U$ и силой постоянного тока $I$ в законе Ома для участка цепи.

Единица сопротивления называется омом (Ом) в честь немецкого ученого Г. Ома, который ввел это понятие в физику. Один ом ($1$ Ом) — это сопротивление такого проводника, в котором при напряжении $1$ В сила тока равна $1$ А.

Удельное сопротивление

Сопротивление однородного проводника постоянного сечения зависит от материла проводника, его длины $l$ и поперечного сечения $S$ и может быть определено по формуле:

где $ρ$ — удельное сопротивление вещества, из которого изготовлен проводник.

Удельное сопротивление вещества — это физическая величина, показывающая, каким сопротивлением обладает изготовленный из этого вещества проводник единичной длины и единичной площади поперечного сечения.

Из формулы $R=ρ/$ следует, что

Величина, обратная $ρ$, называется удельной проводимостью $σ$:

Так как в СИ единицей сопротивления является $1$ Ом, единицей площади $1м^2$, а единицей длины $1$ м, то единицей удельного сопротивления в СИ будет $1$ Ом$·м^2$/м, или $1$ Ом$·$м. Единица удельной проводимости в СИ — $Ом^<-1>м^<-1>$.

На практике площадь сечения тонких проводов часто выражают в квадратных миллиметрах (м$м^2$). В этом случае более удобной единицей удельного сопротивления является Ом$·$м$м^2$/м. Так как $1 мм^2 = 0.000001 м^2$, то $1$ Ом$·$м $м^2$/м$ = 10^<-6>$ Ом$·$м. Металлы обладают очень малым удельным сопротивлением — порядка ($1 ·10^<-2>$) Ом$·$м$м^2$/м, диэлектрики — в $10^<15>-10^<20>$ раз большим.

Зависимость сопротивления от температуры

С повышением температуры сопротивление металлов возрастает. Однако существуют сплавы, сопротивление которых почти не меняется при повышении температуры (например, константан, манганин и др.). Сопротивление же электролитов с повышением температуры уменьшается.

Температурным коэффициентом сопротивления проводника называется отношение величины изменения сопротивления проводника при нагревании на $1°$С к величине его сопротивления при $0°$С:

Зависимость удельного сопротивления проводников от температуры выражается формулой:

В общем случае $α$ зависит от температуры, но если интервал температур невелик, то температурный коэффициент можно считать постоянным. Для чистых металлов $α=(<1>/<273>)K^<-1>$. Для растворов электролитов $α

Закон Кулона: основной закон электростатики кратко и понятно

В данное статье описывается знаменитый закон из молекулярной физики — закон Кулона, название дано в честь ученого, который его открыл. Описывается также правило принципа суперпозиции и границы применимости закона кулоновского взаимодействия.

Закон Кулона определение и формула

Значительная доля явлений, которые совершаются в окружающем нас мире, пока что не имеет объяснения. Физики не сумели их разъяснить даже с помощью механики и молекулярной физики, однако некоторые такие явления можно объяснить силами, которые функционируют между предметами на расстояниях. Массы этих взаимодействующих тел абсолютно не оказывают влияния на конечное значение этих сил. То есть они никак не гравитационные. Эти силы привыкли именовать электромагнитными.

Электростатическое поле формируется покоящимися во времени электрическими зарядами, причем само оно также неизменно во времени.

Закон Кулона — это фундаментальный закон, который открыл в свое время опытным путем ученый, инженер, естествоиспытатель Шарль Кулон. Данное физическое правило позволяет описывать связь двух заряженных предметов, сформулировано оно для абсолютно не двигающихся точечных зарядов в вакууме. Это основной закон электростатики.

Внимание! Точечные заряды — абстракция, в реальной жизни их нет. В физике под этим понятием свыклись иметь в виду заряды, физические размеры которых проигрывают в сравнении с длиной прямой, проведенной между ними.

Формулировка означает следующее: между двумя точечными электрическими зарядами в вакууме есть определенная сила. Она пропорциональна умножению их модулей, деленных на квадрат расстояния. Под расстоянием подразумевается длина прямой, соединяющей данные заряды. Эта сила считается силой взаимодействия, она направлена вдоль отрезка, соединяющего предметы. Кулоновская сила значится силой отталкивающей в случае совпадения знаков зарядов, и силой притяжения, если знаки зарядов являются разными. Заряды, как известно, бывают положительные и отрицательные. Положительный заряд получается путем трения стеклянной палочки о шелк, в то же время отрицательный достигается путем натирания эбонитовой палочки о шерсть.

Иначе записать можно так, где коэффициент в знаменателе — это константа диэлектрической проницаемости.

Коэффициент пропорциональности в законе Кулона

Коэффициент k введен для того, чтобы обеспечить переход из гауссовой системы единиц в международную систему единиц (СИ). В гауссовой системе коэффициент равен 1. В международной — он обратно пропорционален 4-кратному произведению числа ПИ на электрическую постоянную. Электрическая постоянная — это константа, относится к числу фундаментальных физических постоянных. Ее значение примерно равно 8,85418781762⋅10 −12 Ф/м, где Ф — фарад. Записывается электрическая постоянная как E0.

Важно! В тех средах, где пространство заполнено бесконечным однородным диэлектрическим веществом, также добавляют диэлектрическую проницаемость.

Например, для воздуха диэлектрическая проницаемость равна 1,000594.

Значения диэлектрической проницаемости:

Вакуум	1
Воздух	1,000594
Керосин	2
Титанат бария	1200

Закон Кулона в векторной форме

В векторном виде выглядит так:

Пояснения: r₁₂ — радиус-вектор;

Сила кулоновского взаимодействия измеряется в Ньютонах. В системе СИ за единицу заряда принимают 1 Кл, то есть величину заряда, который протекает за 1 секунду в проводнике при силе тока 1 А. 1 Ньютон равен килограмму, помноженному на метр и все это деленное на секунду в квадрате.

Стоит отметить и закон сохранения заряда, который гласит, что алгебраическая сумма величин зарядов замкнутой электрической системы не меняется!

Что можно определить с помощью закона Кулона

Применив данный физический закон, возможно установить значение и направление силы, которая действует на точечный заряд со стороны иного заряда. Также возможно вычислить величины точечных зарядов, значение радиус-вектора между ними.

Для каких заряженных тел справедлив закон

В идеале закон применяют только по отношению к точечным заряженным телам, однако в жизни он также справедлив для заряженных тел, расстояние между которыми превышает в несколько раз непосредственно размеры самих тел. Его применяют для сред, в которых нет свободных зарядов.

Если заряды имеют форму сферы, то полагается, что весь заряд сконцентрирован в центре данной сферы.

Когда вынужденно применяют закон для заряженных тел, то их просто разбивают на множества заряженных точечных зарядов.

Также следует учесть тот факт, что заряды должны быть неподвижными. На те, которые движутся в электрическом поле, начинает действовать помимо силы Кулона еще сила Лоренца, к примеру. Данная сила придает заряженному телу дополнительное ускорение.

Границы применимости закона Кулона

Для того чтобы объяснить грамотно и максимально приближенно к истине поведение зарядов, находящихся в вакууме и являющихся точечными, используют закон Кулона. Тем не менее для реальных тел следует учесть следующие параметры:

• объем и размеры рассматриваемых тел;
• характеристики среды, в которой рассматривают заряженные тела;

Некоторые испытатели в экспериментах наблюдали, что если тело, которое несет небольшой заряд, поместить в электрическое поле другого тела с зарядом большим по значению, оно начинает притягиваться к последнему. В таком случае можно говорить о том, что кулоновское правило неприменимо, так как одноименные заряды должны отталкиваться, а не наоборот. То есть можно сказать, что в вышеописанном эксперименте не работают законы Кулона и сохранения электрического заряда. Скорее всего, физикам еще предстоит узнать, как именно и с помощью чего можно объяснить это явление.

Также на очень маленьких расстояниях, порядка 10–18 м, появляются электрослабые эффекты. Кулоновские силы взаимодействия не работают. Но если внести небольшие поправки, то можно использовать закон Кулона. В сильных электромагнитных полях, к примеру около магнетронов, он также нарушается.

Закон Кулона в вакууме

Максимальное значение кулоновские силы достигают в вакууме. В других же средах добавляется в знаменатель сопротивление среды. Если проще, то чем больше значения зарядов, тем больше сила, если же расстояние между зарядами увеличить и поместить их в отличную от вакуума среду, то сила уменьшится.

Взаимодействие зарядов закон Кулона

Силы взаимодействия между зарядами по модулю принимают одинаковое значение, но отличаются по направлению. Таким образом, напрашивается вывод, что сила взаимодействия относится к тем силам, которые повинуются третьему закону Ньютона: у любой силы есть противодействующая сила, равная ей по модулю, но обратная по направлению.

Между электрическими зарядами одного знака действуют силы отталкивания, а между зарядами разных знаков — силы притяжения. Взаимодействие между зарядами лежит в основе всех фундаментальных законов электродинамики, электромагнетизма, электростатики.

Принцип суперпозиции закон Кулона

Вне зависимости от того, сколько зарядов в системе, можно использовать закон Кулона, чтобы высчитать силу взаимодействия между каждой парой. Отсюда следует принцип суперпозиции, который формулируется примерно так:

На заряд, который расположен в любой точке системы зарядов, действует сила. При этом заряды в системе объединены. Данная сила представляет собой векторную сумму сил, создающихся каждым зарядом системы по отдельности и действующих на заряд в данной точке. К слову, принцип суперпозиции распространяется на любые заряженные тела, не обязательно только на точечные заряды.

Пример: Есть две заряженные точки, которые действуют на третью точку силами: F1 и F2. Тогда система, состоящая из первой и второй точек, действует на третью точку с силой F = F1 + F2.

Также отсюда следует, что напряженность электрического поля, то есть силовая характеристика поля, складывается из суммы напряженностей, которые создаются обособленным зарядом поля.

1) Напряженность равна результату деления кулоновской силы, действующей на заряд, на величину этого заряда.

2) Величина пробного заряда не влияет на напряжённость.

3) Сила, которая действует на заряд от электрического поля, равняется произведению заряда на вектор напряженности в этой точке.

Если рассмотреть с физической точки зрения, данное правило исходит из того, что покоящиеся заряды создают электростатическое поле. Иначе говоря, поля разных зарядов не влияют друг на друга, то есть суммарное поле системы зарядов складывается из векторной суммы электростатических полей, созданных каждым зарядом.

Важно! Следует учесть, что принцип суперпозиции не действует на очень малых или слишком больших расстояниях.

Принцип суперпозиции подразумевает тот факт, что на силы между двумя предметами (подразумеваются силы взаимодействия) не влияет присутствие других тел, обладающих каким-то количеством заряда. Но при этом должно быть задано распределение зарядов.

Задачи на закон Кулона с решением

Заряженный шарик приводят к тому, чтобы он соприкоснулся с точно таким же незаряженным шариком. Находясь на расстоянии r = 15r = 15 см, шарики отталкиваются с силой F = 1F = 1 мН. Какое значение было у первоначального заряда заряженного шарика?

Так как заряд, когда соприкасается, делится на 2 ровные части из-за того, что шарики одинаковые, мы можем рассчитать заряды шаров после соприкосновения. Сила кулоновского взаимодействия нам известна.

Для начала необходимо перевести основные единицы в систему СИ:

Получается, что до соприкосновения заряд заряженного шарика был вдвое больше:

Кл, что равно 10 мкКл.

Два одинаковых маленьких металлических шарика притягиваются с некоторой силой. Шарики привели в соприкосновение и раздвинули на расстояние в n = 2 раза большее, чем прежде. При этом модуль силы взаимодействия уменьшился в m = 5 раз. Найти величину заряда первого шарика до соприкосновения, если второй имел заряд q2 = 1,6 нКл.

Сила кулоновского взаимодействия до того, как шары соприкоснулись:

Из условий задачи известно, что сила после соприкосновения уменьшилась в 5 раз:

Одновременно с этим заряды шаров изменились, то есть:

Одна и та же сила равна:

Следует ввести замену: q1 / q2 = t.

Решаем квадратное уравнение и находим два ответа:

Единицы измерения заряда. Закон Кулона

В результате долгих наблюдений учеными было установлено, что разноименно заряженные тела притягиваются, а одноименно заряженные наоборот – отталкиваются. Это значит, что между телами возникают силы взаимодействия. Французский физик Ш. Кулон опытным путем исследовал закономерности взаимодействия металлических шаров и установил, что сила взаимодействия между двумя точечными электрическими зарядами будет прямопропорциональна произведению этих зарядов и обратно пропорциональна квадрату расстояния между ними:

Где k – коэффициент пропорциональности, зависящий от выбора единиц измерений физических величин, которые входят в формулу, а также и от среды, в которой находятся электрические заряды q₁ и q₂. r – расстояние между ними.

Отсюда можем сделать вывод, что закон Кулона будет справедлив только точечных зарядов, то есть для таких тел, размерами которых вполне можно пренебречь по сравнению с расстояниями между ними.

В векторной форме закон Кулона будет иметь вид:

Где q₁ и q₂ заряды, а r – радиус-вектор их соединяющий; r = |r|.

Силы, которые действуют на заряды, называют центральными. Они направлены по прямой, соединяющей эти заряды, причем сила, действующая со стороны заряда q₂ на заряд q₁, равна силе, действующей со стороны заряда q₁ на заряд q₂, и противоположна ей по знаку.

Для измерения электрических величин могут использоваться две системы счисления – система СИ (основная) и иногда могут использовать систему СГС.

В системе СИ одной из главных электрических величин является единица силы тока – ампер (А), то единица электрического заряда будет ее производной (выражается через единицу силы тока). Единицей определения заряда в СИ является кулон. 1 кулон (Кл) – это количество «электричества», проходящего через поперечное сечение проводника за 1 с при токе в 1 А, то есть 1 Кл = 1 А·с.

Коэффициент k в формуле 1а) в СИ принимается равным:

И закон Кулона можно будет записать в так называемой «рационализированной» форме:

Многие уравнения, описывающие магнитные и электрические явления, содержат множитель 4π. Однако, если данный множитель ввести в знаменатель закона Кулона, то он исчезнет из большинства формул магнетизма и электричества, которые очень часто применяют в практических расчетах. Такую форму записи уравнения называют рационализированной.

Величина ε в данной формуле – электрическая постоянная.

Основными единицами системы СГС являются механические единицы СГС (грамм, секунда, сантиметр). Новые основные единицы дополнительно к вышеперечисленным трем в системе СГС не вводятся. Коэффициент k в формуле (1) принимается равным единице и безразмерным. Соответственно закон Кулона в не рационализированной форме будет иметь вид:

В системе СГС силу измеряют в динах: 1 дин = 1 г·см/с 2 , а расстояние в сантиметрах. Предположим, что q = q₁ = q₂, тогда из формулы (4) получим:

Если r = 1см, а F = 1 дин, то из этой формулы следует, что в системе СГС за единицу заряда принимают точечный заряд, который (в вакууме) действует на равный ему заряд, удаленный от него на расстояние 1 см, с силой в 1 дин. Такая единица заряда называется абсолютной электростатической единицей количества электричества (заряда) и обозначается СГС_q. Ее размерность:

Для вычисления величины ε, сравним выражения для закона Кулона, записанные в системе СИ и СГС. Два точечных заряда по 1 Кл каждый, которые находятся на расстоянии 1 м друг от друга, будут взаимодействовать с силой (согласно формуле 3):

В СГС данная сила будет равна:

Сила взаимодействия между двумя заряженными частицами зависит от среды, в которой они находятся. Чтобы характеризовать электрические свойства различных, сред было введено понятие относительной диэлектрической проницательности ε.

Значение ε это различная величина для разных веществ – для сегнетоэлектриков ее значение лежит в пределах 200 – 100 000, для кристаллических веществ от 4 до 3000, для стекла от 3 до 20, для полярных жидкостей от 3 до 81, для неполярных жидкостей от 1,8 до 2,3; для газов от 1,0002 до 1,006.

Также от температуры окружающей среды зависит и диэлектрическая проницаемость (относительная).

Если учесть диэлектрическую проницаемость среды, в которую помещены заряды, в СИ закон Кулона примет вид:

Диэлектрическая проницаемость ε – величина безразмерная и она не зависит от выбора единиц измерения и для вакуума считается равной ε = 1. Тогда для вакуума закон Кулона примет вид:

Поделив выражение (6) на (5) получим:

Соответственно относительная диэлектрическая проницаемость ε показывает, во сколько раз сила взаимодействия между точечными зарядами в какой-то среде, которые находятся на расстоянии r друг относительно друга меньше, чем в вакууме, при том же расстоянии.

Для раздела электричества и магнетизма систему СГС иногда называют системой Гаусса. До появления системы СГС действовали системы СГСЭ (СГС электрическая) для измерения электрических величин и СГСМ (СГС магнитная) для измерения магнитных величин. В первой равной единице принималась электрическая постоянная ε, а второй магнитная постоянная μ.

В системе СГС формулы электростатики совпадают соответствующими формулами СГСЭ, а формулы магнетизма, при условии, что они содержат только магнитные величины – с соответствующими формулами в СГСМ.

Но если в уравнении одновременно будет содержаться и магнитные, и электрические величины, то данное уравнение, записанное в системе Гаусса, будет отличаться от этого же уравнения, но записанного в системе СГСМ или СГСЭ множителем 1/с или 1/с 2 . Величина с равна скорости света (с = 3·10 10 см/с) называется электродинамической постоянной.

Закон Кулона в системе СГС будет иметь вид:

Пример

На двух абсолютно идентичных каплях масла недостает по одному электрону. Силу ньютоновского притяжения уравновешивает сила кулоновского отталкивания. Нужно определить радиусы капель, если расстояния между ними значительно превышает их линейные размеры.

Решение

Поскольку расстояние между каплями r значительно больше их линейных размеров, то капли можно принять за точечные заряды, и тогда сила кулоновского отталкивания будет равна:

Где е – положительный заряд капли масла, равный заряду электрона.

Силу ньютоновского притяжения можно выразить формулой:

Где m – масса капли, а γ – гравитационная постоянная. Согласно условию задачи F_к = F_н, поэтому:

Масса капли выражена через произведение плотности ρ на объем V, то есть m = ρV, а объем капли радиуса R равен V = (4/3)πR 3 , откуда получаем:

В данной формуле постоянные π, ε, γ известны; ε = 1; также известен и заряд электрона е = 1,6·10 -19 Кл и плотность масла ρ = 780 кг/м 3 (справочные данные). Подставив числовые значения в формулу получим результат: R = 0,363·10 -7 м.

Модули зарядов обозначают, как (|q_1|) и (|q_2|) . В этом случае Закон Кулона можно представить в виде уравнения:

Коэффициент пропорциональности k, согласно закону Кулона, определяется выбором системы единиц.

Полная формула закона Кулона обладает следующим видом:

где (F) — Сила Кулона,

(q_1) и (q_2) являются электрическими зарядами тел;

r — расстояние между зарядами;

(varepsilon _<0>) — электрическая постоянная, равная (8,85*10^<-12>) ;

(varepsilon ) — диэлектрическая проницаемость среды, равная 9*109;

k — коэффициент пропорциональности в законе Кулона.

Силы взаимодействия определяются третьим законом Ньютона:

Данные силы представляют собой силы отталкивания при одинаковых знаках зарядов и силами притяжения при разных знаках. Для обозначения электрических зарядов используют буквы q и Q. Благодаря имеющимся фактам, полученным в результате экспериментов, можно сделать следующие выводы:

1. Имеется два типа электрических зарядов, которые условно обозначают положительными и отрицательными.
2. Допускается передача заряда от одного объекта к другому, так как в отличие от массы, не принадлежат к категории неотъемлемых характеристик тела, поэтому один и тот же объект при разных обстоятельствах может обладать как положительным, так и отрицательным зарядом.
3. Одноименные заряды будут отталкиваться, а разноименные — притягиваться, что подтверждает принципиальную разницу между электромагнитными и гравитационными силами, ведь, благодаря гравитации тела в любом случае притягиваются друг к другу.

Электрическое или кулоновское взаимодействие называют взаимодействием неподвижных электрических зарядов. Существует специальный раздел в электродинамике под названием электростатика, целью которого является изучение кулоновского взаимодействия. Справедливое утверждение закона Кулона распространяется на точечные заряженные тела. В случае когда размеры зарядов намного меньше, чем расстояние между ними, закон Кулона действует на практике. Для его выполнения необходимо соблюдать несколько важных условий:

• точечность зарядов;
• неподвижность зарядов;
• взаимодействие зарядов в вакууме.

Кулоном называют заряд, который проходит за 1 секунду через поперечное сечение проводника при силе тока 1 Ампер.

Единица силы тока — Ампер — относится к основным единицам измерения таким, как длина, время, масса. В Международной системе СИ принято использовать в качестве единицы заряда кулон (Кл).

Применение закона Кулона на практике

Закон Кулона работает во всех областях современной электротехники. Данное утверждение справедливо, начиная с электрического тока, заканчивая простейшим заряженным конденсатором. Простейший случай — введение диэлектрика. Сила, с которой заряды взаимодействуют в вакууме, больше, чем сила взаимодействия аналогичных зарядов, разделенных диэлектрическим материалом.

Диэлектрической проницаемостью среды называют величину для количественного определения сил, независимо от расстояния между зарядами и от их величин. Чтобы рассчитать силу, которая будет действовать в присутствии диэлектрика, необходимо силу взаимодействия зарядов в вакууме поделить на диэлектрическую проницаемость внесенного диэлектрика.

С помощью изучения закона Кулона удается спроектировать сложное исследовательское оборудование в виде ускорителя заряженных частиц. Подобные установки функционируют на механизме взаимодействия электрического поля и заряженных частиц. Энергия частицы увеличивается за счет работы, которую совершает электрическое поле в ускорителе. Закон Кулона в этом случае полностью соблюдается, так как ускоряемую частицу можно рассмотреть в качестве точечного заряда, а действие ускоряющего электрического поля ускорителя представить в виде суммарной силы со стороны других точечных зарядов.

Направление частицы, исходя из силы Лоренца, определяет магнитное поле. Данная сила не воздействует на энергию и траекторию движения частиц в ускорителе.

К наиболее распространенным защитным электротехническим сооружениям относят молниеотводы. Работа данного устройства основана на законе Кулона. Гроза сопровождается появлением на Земле больших индуцированных зарядов. Заряды притягиваются в направлении грозовой тучи. В результате на поверхности планеты образуется мощное электрическое поле. В области острых проводников напряженность поля достигает больших значений. На заостренном наконечнике молниеприемника включается коронный заряд, который притягивается к заряду грозового облака, согласно закону Кулона. Около молниеотвода коронный заряд сильно ионизирует воздух, что приводит к уменьшению напряженности электрического поля вблизи острия. Индуцированные заряды не скапливаются на здании, что снижает вероятность возникновения молний. При ударе молнии заряд полностью будет отведен в землю без повреждения установки.

Примеры решения задач на напряженность электрического поля

Задача 1

В вакуумной среде расположена пара одинаковых положительных точечных зарядов. Расстояние между ними составляет r. Необходимо определить напряженность электрического поля в точке, которая равноудалена на расстояние r от этих зарядов.

Решение:

Исходя из принципа суперпозиции полей, напряженность, которую нужно вычислить, определяется геометрической суммой напряженностей полей, которые создаются зарядами. Формула будет иметь следующий вид:

Модули напряженности полей зарядов определяются таким образом:

Если с помощью векторов первого и второго электрических полей построить параллелограмм, то его диагональ будет обозначать напряженность результирующего поля. Модуль напряженности результирующего поля равен:

Задача 2

Проводящая сфера, радиус (R) которой равен 0,2 метра, обладает зарядом (q) (1,8*10^<-4>) Кл. Сфера находится в вакуумной среде. Необходимо определить:

• модуль напряженности электрического поля (vec) на ее поверхности;
• модуль напряженности электрического поля (vec>) в точке, которая удалена на расстояние (r_1) = 10 метров от центра сферы;
• модуль напряженности (vec>) в центральной точке сферы.

Решение:

Электрическое поле, характерное для заряженной сферы, будет равно полю точечного заряда. Отсюда следует равенство:

Таким образом, искомые величины можно рассчитать:

• (E=kfrac<2>>=4times 10^<7>) (Н/Кл);
• (E=kfrac^<2>>=16times 10^<3>) (Н/Кл);
• напряженность поля в сфере, независимо от местонахождения точки, соответствует нулевому значению, то есть Е0 = 0.

Знание основных физических формул является гарантией успешного решения задач не только школьной программы, но и вуза. Если в процессе обучения и постижения законов физики у студентов возникают проблемы, то решение есть. Можно воспользоваться сервисом Феникс.Хелп, чтобы сэкономить массу времени и получить результат высокого качества.

Консультации по выполнению всех типов работ

∀ x, y, z

Поток напряженности электрического поля, проходящий через замкнутую поверхность, пропорционален суммарному электрическому заряду, содержащемуся внутри этой поверхности.

В науке часто бывает, что один и тот же закон можно сформулировать по-разному. По большому счету, от формулировки закона ничего не меняется с точки зрения его действия, однако новая формулировка помогает теоретикам несколько иначе интерпретировать закон и испытать его применительно к новым природным явлениям. Именно такой случай мы и наблюдаем с теоремой Гаусса, которая, по существу, является обобщением закона Кулона, который, в свою очередь, явился обобщением всего, что ученые знали об электростатических зарядах на момент, когда он был сформулирован.

Вообще говоря, в математике, физике и астрономии найдется немного областей, развитию которых не посодействовал замечательный гений Карла Фридриха Гаусса. В 1831 году он вместе со своим молодым коллегой Вильгельмом Вебером (Wilhelm Weber, 1804–1891) занялся изучением электричества и магнетизма и вскоре сформулировал и доказал теорему, названную его именем. Чтобы понять, в чем заключается ее смысл, представьте себе изолированный точечный электрический заряд . А теперь представьте, что он окружен замкнутой поверхностью. Форма поверхности в теореме не важна — это может быть пусть даже сдутый воздушный шарик. В каждой точке окружающей заряд поверхности, однако, наблюдается электрическое поле, образованное зарядом, а произведение напряженности этого электрического поля на сколь угодно малую единицу площади окружающей заряд поверхности, через которую проходят силовые линии поля, называется потоком напряженности электрического поля, и можно рассчитать поток напряженности, приходящийся на каждый элемент поверхности. Теорема Гаусса как раз и гласит, что суммарный поток напряженности электрического поля, проходящий через окружающую заряд поверхность, пропорционален величине заряда.

Связь между законом Кулона и теоремой Гаусса станет очевидной на простом примере. Предположим, что заряд окружен сферой радиуса . На удалении от заряда напряженность электрического поля, которая определяется силой притяжения или отталкивания единичного заряда, помещенного в соответствующую точку, составит, согласно закону Кулона:

Это и есть теорема Гаусса.

Интересное следствие из нее получается, если применить эту теорему к сплошному металлу. Представьте себе цельнометаллический предмет и воображаемую замкнутую поверхность внутри него. Полный электрический заряд внутри такой поверхности будет нулевым, поскольку внутри окажется равное число положительных и отрицательных зарядов — протонов атомных ядер и электронов соответственно. Следовательно, поток напряженности электрического поля, проходящий через такую замкнутую поверхность, также будет равен нулю. Поскольку это верно для любой замкнутой поверхности внутри металла, это означает, что внутри металла не существует и не может существовать электрического поля.

Это свойство металлов часто используется экспериментаторами и инженерами-связистами для защиты высокочувствительных приборов от наведенных извне электрических помех. Обычно прибор просто окружается защитным медным экраном. Согласно теореме Гаусса, внешние электрические поля просто не в состоянии проникнуть внутрь такой оболочки и создать помехи работе прибора.

Другое интересное следствие теоремы Гаусса заключается в том, что если в дороге вас застала гроза, самое безопасное для вас — не выходить из машины, поскольку там вы окружены цельнометаллическим экраном. Даже если в ваш автомобиль ударит молния, внутри вам ничего не будет угрожать, поскольку весь разряд пройдет по корпусу и уйдет в землю. Резина, скорее всего, сгорит, зато сами вы останетесь в целости и сохранности.

Энциклопедия Джеймса Трефила «Природа науки. 200 законов мироздания».
Джеймс Трефил — профессор физики университета Джорджа Мэйсона (США), один из наиболее известных западных авторов научно-популярных книг.