Для чего нужен расчет магнитной цепи?
Расчеты магнитных цепей
 В электрических машинах и аппаратах магнитный поток Ф сосредоточивается в магнитопроводе (ферромагнитном сердечнике) и воздушных зазорах этого магнитопровода. Этот путь магнитного потока называется магнитной цепью.
В электрических машинах и аппаратах магнитный поток Ф сосредоточивается в магнитопроводе (ферромагнитном сердечнике) и воздушных зазорах этого магнитопровода. Этот путь магнитного потока называется магнитной цепью.
Магнитная цепь подобна электрической цепи. Магнитный поток Ф напоминает электрический ток I, индукция B напоминает плотность тока, намагничивающая сила (н. с.) Fн (H∙l=I∙ω) соответствует э. д. с.
В простейшем случае магнитная цепь имеет везде одинаковое сечение и выполнена из однородного магнитного материала. Для определения н. с. l∙ω, необходимой для обеспечения требуемой индукции B, по кривой намагничивания определяют соответствующую напряженность H и умножают ее на среднюю длину магнитной силовой линии l: H∙l=I∙ω=Fм.
Отсюда определяют требуемый ток I или число витков ω катушки.
Сложная магнитная цепь обычно имеет участки с разными сечениями и магнитными материалами. Эти участки обычно соединены последовательно, поэтому по каждому из них проходит одинаковый магнитный поток Ф. Индукция B на каждом участке зависит от сечения участка и рассчитывается для каждого участка в отдельности по формуле B=Ф∶S.
Для разных значений индукции по кривой намагничивания определяют напряженность H и умножают ее на среднюю длину силовой линии соответствующего участка цепи. Суммируя отдельные произведения, получают полную н. с. магнитной цепи:
Fм=I∙ω=H1 ∙l1+H2 ∙l2+H3 ∙l3+. по которой определяют намагничивающий ток или число витков катушки.
1. Каким должен быть намагничивающий ток I катушки, имеющей 200 витков, чтобы ее н. с. создала в чугунном кольце магнитный поток Ф=15700 Мкс =0,000157 Вб? Средний радиус чугунного кольца r=5 см, а диаметр его сечения d=2 см (рис. 1).
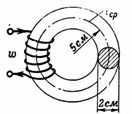
Сечение магнитной цепи S=(π∙d^2)/4=3,14 см 2 .
Индукция в сердечнике равна: B=Ф∶S=15700∶3,14=5000 Гс.
В системе МКСА индукция равна: B=0,000157 Вб :0,0000314 м2 =0,5 Тл.
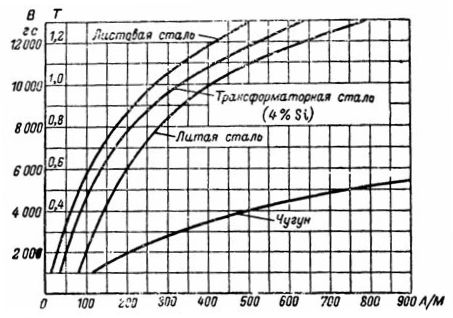
По кривой намагничивания чугуна находим для B=5000 Гс =0,5 Тл требуемую напряженность H, равную 750 А/м. Намагничивающая сила равна: I∙ω=H∙l=235,5 Ав.
Отсюда требуемый ток I=(H∙l)/ω=235,5/200=1,17 А.
2. Замкнутая магнитная цепь (рис. 2) выполнена из пластин трансформаторной стали. Сколько витков должна иметь катушка с током 0,5 А, чтобы создать в сердечнике магнитный поток Ф=160000 Мкс =0,0016 Вб?
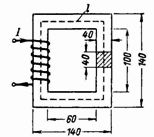
Сечение сердечника S=4∙4=16 см2 =0,0016 м 2 .
Индукция в сердечнике B=Ф/S=160000/16=10000 Гс =1 Тл.
По кривой намагничивания трансформаторной стали находим для B=10000 Гс =1 Тл напряженность H=3,25 А/см =325 А/м.
Средняя длина магнитной силовой линии l=2∙(60+40)+2∙(100+40)=480=0,48 м.
Намагничивающая сила Fм=I∙ω=H∙l=3,25∙48=315∙0,48=156 Ав.
При токе 0,5 А число витков ω=156/0,5=312.
3. Магнитная цепь, изображенная на рис. 3, аналогична магнитной цепи предыдущего примера, за исключением того, что она имеет воздушный зазор δ=5 мм. Какими должны быть н. с. и ток катушки, чтобы магнитный поток был таким же, как и в предыдущем примере, т. е. Ф=160000 Мкс = 0,0016 Вб?
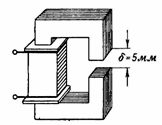
Магнитная цепь имеет два последовательно соединенных участка, сечение которых такое же, как и в предшествующем примере, т. е. S=16 см2. Индукция также равна B=10000 Гс =1 Тл.
Средняя длина магнитной линии в стали немного меньше: lс=48-0,5=47,5 см ≈0,48 м.
Магнитное напряжение на этом участке магнитной цепи Hс ∙lс=3,25∙48≈156 Ав.
Напряженность поля в воздушном зазоре равна: Hδ=0,8∙B=0,8∙10000=8000 А/см.
Магнитное напряжение на участке воздушного зазора Hδ∙δ=8000∙0,5=4000 Ав.
Полная н. с. равна сумме магнитных напряжений на отдельных участках: I∙ω=Hс ∙lс+Hδ∙δ=156+4000=4156 Ав. I=(I∙ω)/ω=4156/312=13,3 А.
Если в предыдущем примере необходимый магнитный поток обеспечивался током 0,5 А, то для магнитной цепи с воздушным зазором 0,5 см требуется ток 13 А, чтобы получить тот же магнитный поток. Отсюда видно, что воздушный зазор, даже незначительный по отношению к длине магнитопровода, сильно увеличивает необходимые н. с. и ток катушки.
4. Расчетом найдено, что магнитный поток трансформатора Ф=72000 Мкс. Требуется рассчитать н. с. и намагничивающий ток первичной обмотки, имеющей 800 витков. В сердечнике трансформатора имеется зазор δ=0,2 мм. Размеры сердечника трансформатора показаны на рис. 4. Сечение сердечника S=2∙3=6 см 2 (трансформаторы с сердечниками такой формы называются броневыми).
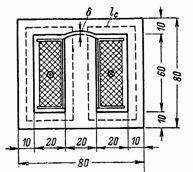
Индукция в сердечнике и воздушном зазоре B=Ф/S=72000/6=12000 Гс.
По кривой намагничивания трансформаторной стали для B=12000 Гс определяем напряженность: Hс=5 А/см.
Средняя длина магнитной линии в стали lс=2∙(6+3)=18 см.
Напряженность в воздушном зазоре Hδ=0,8∙B=9600 А/см.
Намагничивающая сила I∙ω=Hс∙lс+Hδ∙δ=5∙18+9600∙0,02=90+192=282 Ав; I= (I∙ω)/ω=282/800=0,35 А.
В броневом сердечнике магнитный поток разветвляется на две части, замыкающиеся по боковым стержням, сечение которых равно S/2, а средняя длина магнитной линии lс. В результате магнитная цепь полностью аналогична магнитной цепи обычного трансформатора с общим сердечником сечением S и длиной силовой линии lс.
5. Магнитный поток машины постоянного тока Ф=1280000 Мкс. Магнитная цепь содержит ярмо из литой стали со средней длиной магнитной линии lя=80 см, ротор, набранный из пластин электротехнической стали со средней длиной силовой линии lр=18 см, и два воздушных зазора δ по 0,2 см. Сечение ярма и полюса Sя=8∙20 см 2 ; сечение ротора и полюсного наконечника Sр=12∙20 см 2 . Рассчитать н. с. и число витков полюсной катушки, если максимальный ток намагничивания (возбуждения) в ней равен 1 А (рис. 5).
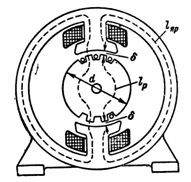
Индукция в ярме и полюсе Bя=Ф/Sя =1280000/160=8000 Гс.
Напряженность в ярме и полюсе согласно кривой намагничивания литой стали при Bя=8000 Гс равна:
Намагничивающая сила на участке ярма Hя∙lя=2,8∙80=224 Ав.
Индукция в роторе, полюсном наконечнике и воздушном зазоре Bр=Ф/Sр =1280000/240=5333 Гс.
Напряженность в роторе из стальных пластин при Bр=5333 Гс Hр=0,9 А/см,
а магнитное напряжение на участке ротора Hр∙lр=0,9∙18=16,2 Ав.
Напряженность в воздушном зазоре Hδ=0,8∙Bδ=0,8∙5333=4266,4 А/см.
Магнитное напряжение на участке воздушного зазора Hδ∙2∙δ=4266,4∙2∙0,2=1706,56 А.
Полная н. с. равна сумме магнитных напряжений на отдельных участках: I∙ω=Hя∙lя+Hр∙lр+Hδ∙2∙δ; I∙ω=224+16,2+1706,56=1946,76 Ав.
Число витков в обеих полюсных катушках ω=(I∙ω)/I=1946,76/1≈2000.
Для чего нужен расчет магнитной цепи
Для некоторых технических целей, пример пары из них мы здесь рассмотрим, требуется рассчитывать параметры магнитных цепей. И главным инструментом в этих расчетах служит закон полного тока. Он звучит так: линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, этим контуром охватываемых. Закон полного тока записывается так:
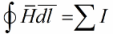
А если при этом контур интегрирования охватывает катушку из W витков, по которой течет ток I, то алгебраическая сумма токов есть произведение I*W – это произведение называется магнитодвижущей силой МДС, которая обозначается F. Данное положение запишем так:
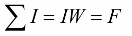
Контур интегрирования зачастую выбирают таким, что он совпадает с силовой линией магнитного поля, в этом случае векторное произведение заменяется на обычное произведение скалярных величин, интеграл заменяют суммой произведений H*L, далее выбирают участки магнитной цепи так, чтобы напряженности H вдоль них можно было бы считать постоянными. Тогда закон полного тока принимает более простой вид:
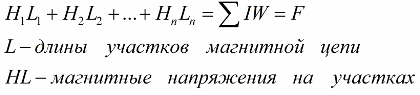
Здесь, кстати, вводят понятие «магнитное сопротивление», определяемое как отношение магнитного напряжения H*L на данном участке к магнитному потоку Ф на нем:
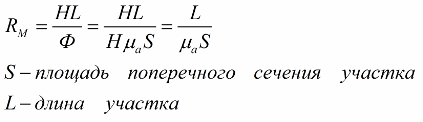
Для примера рассмотрим магнитную цепь, изображенную на рисунке. Здесь ферромагнитный сердечник имеет по всей своей длине одну и ту же площадь поперечного сечения S. Имеет определенную длину средней силовой лини магнитного поля L, а также воздушный зазор известной величины сигма. По обмотке, намотанной на данный магнитопровод, течет определенный намагничивающий ток I.
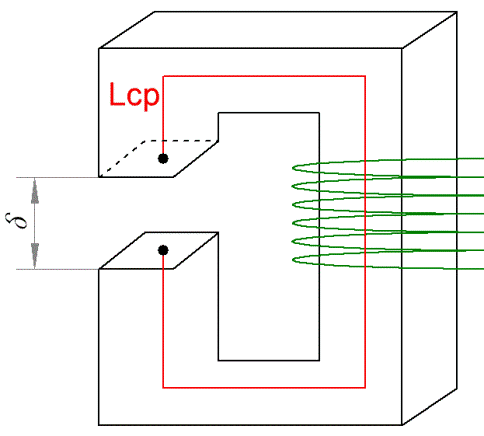
В прямой задаче по расчету магнитной цепи, исходя из заданного магнитного потока Ф в магнитопроводе, находят величину МДС F. Сначала определяют индукцию B в магнитопроводе, для этого делят магнитный поток Ф на площадь сечения S магнитопровода.
Вторым шагом по кривой намагничивания находят величину напряженности H магнитного поля, соответствующую данной величине индукции B. Затем записывают закон полного тока, в который включают все участки магнитной цепи:
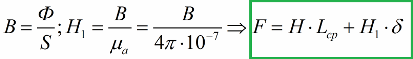
Пример прямой задачи
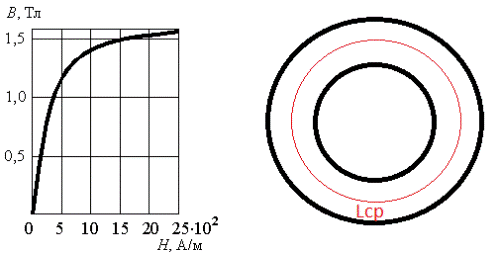
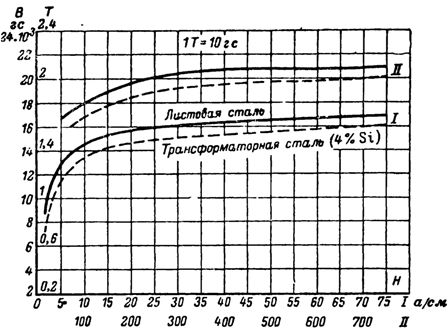
Допустим, есть замкнутый магнитопровод — тороидальный сердечник из трансформаторной стали, индукция насыщения в нем составляет 1,7 Тл. Необходимо найти ток намагничивания I, при котором сердечник войдет в насыщение, если известно, что обмотка содержит W=1000 витков. Длина средней линии равна Lср = 0,5 м. Дана кривая намагничивания.
Находим H по кривой намагничивания: H=2500А/м.
Следовательно I=H*Lср/W=2500*0,5/1000=1,25 (ампер).
Примечание. Аналогичным образом решаются задачи с немагнитным зазором, тогда в левой части уравнения будет сумма всех HL для участков магнитопровода и для участка зазора. Напряженность магнитного поля в зазоре находится делением магнитного потока (по магнитной цепи он везде один и тот же) на площадь зазора и на магнитную проницаемость в зазоре.
Обратная задача по расчету магнитной цепи предполагает, что исходя из известной магнитодвижущей силы F необходимо найти величину магнитного потока.
Для решения этой задачи иногда прибегают к магнитной характеристике цепи МДС F = f(Ф), где нескольким значениям магнитного потока Ф соответствует каждому свое значение МДС F. Так исходя из F можно найти значение магнитного потока Ф.
Пример обратной задачи
На замкнутый тороидальный магнитопровод (как в предыдущей прямой задаче) из трансформаторной стали намотана обмотка из W=1000 витков, по обмотке течет ток I=1,25 ампер. Длина средней линии равна L=0,5 м. Сечение магнитопровода S = 35 кв.см. Найти магнитный поток Ф в сердечнике, пользуясь приведенной кривой намагниченности.
МДС F=I*W=1,25*1000=1250 ампер-виток. F=HL, значит H=F/L=1250/0,5=2500А/м.
По кривой намагничивания находим, что при данной напряженности индукция составляет B = 1,7 Тл.
Магнитный поток Ф=B*S, значит Ф=1,7*0,0035=0,00595 Вб.
Примечание. Магнитный поток по всей неразветвленной магнитной цепи будет одинаковым, и даже если есть воздушный зазор, то в нем магнитный поток будет тем же, подобно току в электрической цепи. См. Закон Ома для магнитной цепи.
Для чего нужен расчет магнитной цепи?
Магнитной цепью называют совокупность тел или сред, по которым замыкается магнитный поток .
Для любого участка магнитной цепи можно получить выражение, устанавливающее связь между магнитным потоком, МДС, действующей в данной цепи, а также ее геометрическими размерами, пользуясь понятием магнитного потока и законом полного тока .
Пусть имеется цилиндрическая катушка с числом витков w , по которым протекает ток i (рис. 1). Выделим трубку магнитного потока, охватывающую все витки катушки, и определим МДС вдоль ее контура
но в изотропной среде направление векторов B и H совпадает. Поэтому вектор H направлен по касательной к оси трубки и cos a =1. Отсюда
В тоже время, элементарный магнитный поток, проходящий через сечение перпендикулярное оси трубки, и напряженность магнитного поля равны
Подставим полученное выражение для напряженности в выражение (2) и с учетом того, что элементарный поток d Ф вдоль трубки имеет постоянное значение, получим
Если распространить приведенные рассуждения на весь магнитный поток катушки, то при условии, что размеры сечений магнитных трубок существенно меньше их длины, из выражения (4) будем иметь:
где величина называется магнитным сопротивлением . В этом выражении m — абсолютная магнитная проницаемость среды; l — длина средней линии, т.е. линии проходящей через центр поперечного сечения магнитопровода s . Магнитное сопротивление измеряется в [Гн -1 ]
В выражении (5) магнитный поток Ф связан с МДС F и магнитным сопротивлением R m аналогично тому, как связаны между собой электрический ток, ЭДС и сопротивление в выражении закона Ома. Однако сходство между этими законами чисто формальное, т.к. они существенно различаются между собой. Электрическое сопротивление может быть бесконечно большим и в этом случае возможно существование ЭДС без протекания электрического тока в цепи. Магнитное сопротивление всегда конечно и наличие МДС означает одновременное обязательное существование магнитного потока .
Обычно для расчета магнитных цепей применяют закон полного тока. Если разбить магнитную цепь на участки так, чтобы в пределах каждого из них площадь поперечного сечения и магнитная среда были одинаковыми, то можно считать, что магнитный поток проходит по каждому участку вдоль его средней линии. При этом индукция в пределах каждого участка будет постоянной, следовательно, постоянной будет и напряженность магнитного поля. Тогда в левой части выражения (2) интеграл вдоль замкнутого контура, проходящего по средним линиям сечений всех участков магнитной цепи, можно представить суммой
где p — число участков магнитной цепи длиной l , в пределах которых H =const; n — число обмоток, охватываемых средней линией контура, с числом витков w и током I .
Произведение Hl = U м называется магнитным падением напряжения или магнитным напряжением , а Iw = F является МДС. Пользуясь этими понятиями, можно представить выражение (6) в форме аналогичной второму закону Кирхгофа для электрических цепей
т.е. сумма падений магнитного напряжения вдоль замкнутого контура магнитной цепи равна алгебраической сумме МДС катушек, охватываемых контуром .
Однако следует заметить, что Г.Р.Кирхгоф этот закон не формулировал и он является формальной аналогией.
Другой формальной аналогией законам Кирхгофа, вытекающей из принципа непрерывности магнитного потока, является равенство нулю алгебраической суммы магнитных потоков в узлах магнитной цепи .
Например, если магнитопровод разделяется на части (рис. 3), то разделяется на составляющие Ф 1 и Ф 2 магнитный поток Ф. Поскольку магнитный поток через любую замкнутую поверхность равен нулю, то окружив разветвление магнитопровода такой произвольной поверхностью получим
Первая запись соответствует некоторому соглашению о знаках магнитных потоков. Например, можно считать потоки направленные к узлу положительными, а от узла отрицательными. Вторая запись объединяет в левую и правую части равенства потоки с одинаковой ориентацией.
Следует заметить, что выражение (8) справедливо только при условии, что магнитный поток не ответвляется через боковые поверхности магнитопровода в окружающую среду.
Понятие магнитного сопротивления можно использовать для расчетов магнитных цепей с ферромагнетиками только в том случае, если вещество ненасыщено , т.к. в противном случае входящее в него значение магнитной проницаемости m зависит от Ф.
Если разбить магнитную цепь (рис 2 а)) на участки с одинаковой площадью поперечного сечения и веществом, то каждый такой участок можно представить магнитным сопротивлением в соответствии с выражением (5) . Катушку с током I можно представить МДС равной F = Iw .
В результате этих преобразований, исходная магнитная цепь будет представлена электрической схемой замещения (рис. 2 б)), в которой роль токов будут играть магнитные потоки на соответствующих участках. К этой схеме формальной можно применить все законы и методы расчета электрических цепей.
При расчете магнитной цепи с ферромагнетиком в общем случае нужно иметь данные о геометрических размерах и материале магнитопровода. Задача расчета может формулироваться в двух вариантах, называемых прямой и обратной задачей . В первом случае по заданному на каком-либо участке магнитному потоку или индукции нужно определить МДС, необходимую для создания этого потока. В обратной задаче по заданной МДС нужно определить магнитный поток или индукцию на каком-либо участке.
Обратная задачи существенно отличаются от прямой, т.к. может быть решена только методом последовательных приближений.
При расчетах магнитных цепей обычно делают следующие допущения:
- весь магнитный поток проходит по магнитопроводу, не ответвляясь в окружающую среду, т.е. пренебрегают т.н. потоком рассеяния;
- в воздушных зазорах пересекающих магнитопровод отсутствует выпучивание магнитных линий, т.е. поперечное сечение магнитного потока в зазорах считают равным сечению магнитопровода.
Рассмотрим магнитную цепь, приведенную на рис. 4 а). Пусть для этой цепи требуется определить МДС обмотки, обеспечивающую в воздушном зазоре cd магнитный поток с плотностью B cd =1,5 Тл. Геометрические размеры магнитопровода приведены в таблице 1.
Потоком рассеяния мы пренебрегаем и считаем, что весь магнитный поток замыкается по магнитопроводу из ферромагнетика, кривая намагничивания которого приведена на рис. 4 б).
Разобьем магнитопровод на участки с одинаковыми площадями поперечного сечения, что обеспечит выполнение условия H =const в пределах каждого участка.
По заданной площади поперечного сечения магнитопровода на участках bc и de найдем значение магнитного потока в зазоре как Ф = B cd S cd = 1,5 Ч 1,0 Ч 10 -4 = 1,5 Ч 10 -4 Вб.
Для участков bc и de , имеющих сечение равное воздушному зазору, плотность магнитного потока будет равна заданной плотности в зазоре, а для участков ab , ef и af определим плотность как отношение потока Ф к площади поперечного сечения соответствующего участка.
Для воздушного зазора магнитная проницаемость m является константой. Поэтому для любого воздушного промежутка напряженность магнитного поля H в А/м однозначно определяется через индукцию (плотность магнитного потока) B в Тл в виде
Далее для всех участков магнитопровода по значению плотности магнитного потока B с помощью кривой намагничивания рис. 4 б) определим напряженность магнитного поля H и, умножив ее на длины соответствующих участков найдем падения магнитного напряжения. Результаты этих вычислений сведены в таблицу.
9. Магнитные цепи
9.1. Основные определения
Как известно из курса физики, вокруг проводника с током появляется магнитное поле. Интенсивность магнитного поля характеризуется векторной величиной: напряженностью магнитного поля 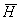 , измеряемой в амперах на метр (A/м). Интенсивность магнитного поля характеризуется также вектором магнитной индукции
, измеряемой в амперах на метр (A/м). Интенсивность магнитного поля характеризуется также вектором магнитной индукции 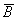 , измеряемой в теслах (Тл). Напряженность магнитного поля не зависит, а магнитная индукция зависит от свойств окружающей среды.
, измеряемой в теслах (Тл). Напряженность магнитного поля не зависит, а магнитная индукция зависит от свойств окружающей среды.
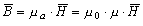
где μ — абсолютная магнитная проницаемость, Гн/м;
μ — относительное значение магнитной проницаемости, безразмерная величина;
μ = 4π·10 -7 Гн/м.
В зависимости от величины относительной магнитной проницаемости, все вещества делятся на три группы.
К первой группе относятся диамагнетики: вещества, у которых μ 1.
К третьей группе относятся ферромагнетики, вещества с μ >> 1.
К ферромагнетикам принадлежат железо, никель, кобальт и многие сплавы из неферромагнитных веществ.
Магнитной цепью называется совокупность устройств, содержащих ферромагнитные вещества. Процессы в магнитных цепях описываются с помощью понятий магнитодвижущей силы, магнитного потока.
Магнитным потоком называется поток вектора магнитной индукции через поверхность S
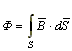 .
.
Магнитный поток измеряется в веберах (Вб).
Источником магнитодвижущей силы является либо постоянный магнит, либо электромагнит (катушка, обтекаемая током).
Магнитодвижущая сила электромагнита
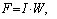
где I — ток, протекающий в катушке;
W — число витков катушки.
В магнитных цепях используется свойство ферромагнитного материала тысячекратно усиливать магнитное поле катушки с током за счет собственной намагниченности.
9.2. Свойства ферромагнитных материалов
Поместим ферромагнитный материал внутри катушки с током. Сначала, с увеличением напряженности намагничивающего поля, магнитная индукция быстро возрастает. Затем, из-за насыщения материала, при дальнейшем увеличении напряженности магнитного поля магнитная индукция почти не меняется. При уменьшении напряженности намагничивающего поля кривая размагничивания не совпадает с кривой намагничивания из-за явления гистерезиса. Явление гистерезиса заключается в том, что изменение магнитной индукции запаздывает от изменения намагничивающего поля. Кривая зависимости B(H), получающаяся при циклическом перемагничивании ферромагнитного материала, называется петлей гистерезиса. Эта кривая изображена на рис. 9.1. Чем больше площадь петли, тем больше потери на перемагничивание, нагревающие материал.
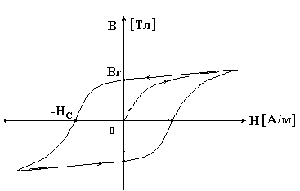
Значение магнитной индукции при напряженности намагничивающего поля, равном нулю, называется остаточной магнитной индукцией Br, или остаточной намагниченностью.
Напряженность магнитного поля НС при В = 0 называется коэрцитивной силой.
Ферромагнитные материалы с большим значением коэрцитивной силы (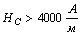 ) называются магнитотвердыми. Из этих материалов изготавливают постоянные магниты.
) называются магнитотвердыми. Из этих материалов изготавливают постоянные магниты.
Ферромагнитные материалы с малым значением коэрцитивной силы (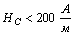 ) называются магнитомягкими. Эти материалы используют в магнитопроводах электрических машин и трансформаторов.
) называются магнитомягкими. Эти материалы используют в магнитопроводах электрических машин и трансформаторов.
Таким образом, зависимости B = f(H) у ферромагнитных материалов нелинейные.
Эти зависимости приводятся в справочниках в табличной форме или в виде кривых, называемых кривыми намагничивания.
9.3. Расчет магнитных цепей
Основным законом, используемым при расчетах магнитных цепей, является закон полного тока.
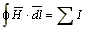 (9.1)
(9.1)
Он формулируется следующим образом: линейный интеграл вектора напряженности магнитного поля по замкнутому контуру равен алгебраической сумме токов, охватываемых этим контуром. Если контур интегрирования охватывает катушку с числом витков W, через которую протекает ток I, то алгебраическая сумма токов 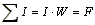 , где F — магнитодвижущая сила.
, где F — магнитодвижущая сила.
Обычно контур интегрирования выбирают таким образом, чтобы он совпадал с силовой линией магнитного поля, тогда векторное произведение в формуле (9.1) можно заменить произведением скалярных величин H·dl. В практических расчетах интеграл 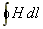 заменяют суммой
заменяют суммой 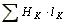 и выбирают отдельные участки магнитной цепи таким образом, чтобы H1, H2, . . . вдоль этих участков можно было считать приблизительно постоянными. При этом (9.1) переходит в
и выбирают отдельные участки магнитной цепи таким образом, чтобы H1, H2, . . . вдоль этих участков можно было считать приблизительно постоянными. При этом (9.1) переходит в
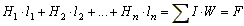 (9.2)
(9.2)
где l1, l2, …, ln — длины участков магнитной цепи;
H1·l1, H2·l2 — магнитные напряжения участков цепи. Магнитным сопротивлением участка магнитной цепи называется отношение магнитного напряжения рассматриваемого участка к магнитному потоку в этом участке
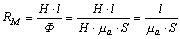 ,
,
где S — площадь поперечного сечения участка магнитной цепи,
l — длина участка.
Рассмотрим расчет магнитной цепи, изображенной на рис. 9.2.
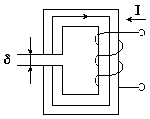 Ферромагнитный магнитопровод имеет одинаковую площадь поперечного сечения S.
Ферромагнитный магнитопровод имеет одинаковую площадь поперечного сечения S.
lср — длина средней силовой линии магнитного поля в магнитопроводе;
δ — толщина воздушного зазора.
На магнитопроводе размещена обмотка, по которой протекает ток I.
Рис. 9.2
Прямая задача расчета магнитной цепи заключается в том, что задан магнитный поток Ф и требуется определить магнитодвижущую силу F. Определим магнитную индукцию в магнитопроводе
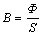 .
.
По кривой намагничивания найдем значение напряженности магнитного поля H, соответствующее величине В.
Напряженность магнитного поля в воздушном зазоре
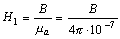 .
.
Магнитодвижущая сила обмотки
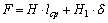 .
.
Магнитные цепи
Электрический ток связан с магнитным полем. Основными величинами, характеризующими магнитное поле, являются: магнитный поток, магнитная индукция и напряженность магнитного поля.
В качестве силовой характеристики магнитного поля вводится векторная величина В, называемая индукцией магнитного поля или просто индукцией. Модуль вектора индукции магнитного поля равен отношению магнитной силы F, направленной вдоль радиуса-вектора, соединяющего точечные заряды, к произведению заряда Q на его скорость v при условии, что заряд движется перпендикулярно вектору индукции:
Единицу индукции магнитного поля называют тесла (Тл): 1 Тл — это индукция поля, которое действует на заряд 1 Кл, движущийся со скоростью 1 м/с перпендикулярно вектору индукции, с поперечной силой 1 Н.
Напряженностью Н магнитного поля называют величину:
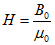
Единицей напряженности магнитного поля служит ампер на метр (А/м).
Другой важной характеристикой магнитного поля является величина, называемая магнитным потоком:
Единицу магнитного потока называют вебер (Вб): 1 Вб — магнитный поток, пронизывающий поверхность площадью 1 метр кв., расположенную перпендикулярно силовым линиям однородного магнитного поля с индукцией 1 Тл.
Напряженность магнитного поля связана с магнитной индукцией соотношением
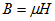
Магнитная проницаемость вещества 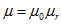
Относительная магнитная проницаемость 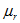
Магнитная проницаемость в вакууме 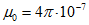
Магнитная проницаемость — безразмерная величина. Таким образом, каждое данное вещество может характеризоваться присущей ему магнитной проницаемостью, так же как диэлектрик — диэлектрической проницаемостью.
Все тела, помещаемые в магнитное поле, изменяют его индукцию.
В 50-х годах прошлого столетия Фарадей обнаружил, что все тела обладают магнитными свойствами, но степень и характер их взаимодействия с полем у различных веществ различны. В связи с этим различают вещества с парамагнитными, диамагнитными и ферромагнитными свойствами.
- диамагнетики
 (висмут, вода, водород, медь, стекло);
(висмут, вода, водород, медь, стекло);
- парамагнетики
 (кислород, платина, вольфрам, алюминий);
(кислород, платина, вольфрам, алюминий);
- ферромагнетики
 (железо, кобальт, чугун, никель).
(железо, кобальт, чугун, никель).
У диамагнетиков, как и у парамагнетиков, зависимость В(Н) (кривая намагничивания) является линейной, отличие только в угле наклона графика.
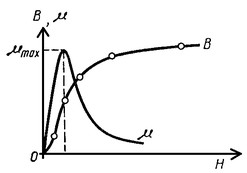 Кривая намагничивания показывает связь между магнитной индукцией и напряженностью магнитного поля. У ферромагнетиков эта связь существенно нелинейная.
Кривая намагничивания показывает связь между магнитной индукцией и напряженностью магнитного поля. У ферромагнетиков эта связь существенно нелинейная.
Индукция поля в намагниченном ферромагнетике сначала быстро нарастает с ростом напряженности внешнего магнитного поля. Затем рост индукции поля замедляется.
В стали потери на перемагничивание пропорциональны площади, ограниченной кривой намагничивания. Материалы с большой площадью кривой намагничивания называются магнитотвердыми, с малой площадью кривой намагничивания — магнитомягкими, например, электротехническая сталь.
Важное отличие ферромагнетиков также заключается в том, что если пара- или диамагнитные свойства вещества проявляются у газов и жидкостей, то ферромагнитные свойства наблюдают только у кристаллов.
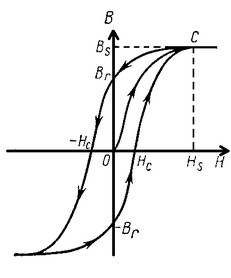 Характерным свойством ферромагнетиков является гистерезис. Явление заключается в том, что индукция ферромагнетика В зависит не только от напряженности намагничивающего поля в данный момент, но и от предварительного намагничивания образца. Поэтому вообще нельзя указать, какая индукция ферромагнетика соответствует данному значению напряженности намагничивающего поля, если неизвестно, в каком состоянии он до этого находился. То же, естественно, относится к значениям магнитной проницаемости.
Характерным свойством ферромагнетиков является гистерезис. Явление заключается в том, что индукция ферромагнетика В зависит не только от напряженности намагничивающего поля в данный момент, но и от предварительного намагничивания образца. Поэтому вообще нельзя указать, какая индукция ферромагнетика соответствует данному значению напряженности намагничивающего поля, если неизвестно, в каком состоянии он до этого находился. То же, естественно, относится к значениям магнитной проницаемости.
Участок ОС кривой на графике характеризует ход первоначальной намагниченности, т. е. случая, когда ферромагнетик был сначала нагрет выше точки Кюри и тем самым полностью размагничен, а затем охлажден и подвергнут намагничиванию. Совершенно иной вид будет иметь кривая намагничения, если ферромагнетик был уже ранее намагничен.
Изготовим сердечник в форме тороида из размагниченного ферромагнетика и обмотаем его равномерно проводником. Меняя силу тока в обмотке, мы тем самым меняем напряженность намагничивающего поля. Пусть напряженность поля возрастет до значения Hs. Этому значению поля соответствует индукция насыщения, равная Bs. Будем уменьшать силу тока в обмотке, уменьшая тем самым напряженность намагничивающего поля. Мы убедимся, что индукция сердечника в процессе размагничивания остается все время большей, чем в процессе намагничивания.
Когда сила тока в обмотке станет равной нулю, исчезнет и намагничивающее поле. Но индукция ферромагнетика не обратится в нуль — сердечник сохранит некоторую остаточную индукцию Вr. И только в том случае, когда по обмотке будет пропущен ток обратного направления и возникнет поле с напряженностью — Нc, индукция сердечника обратится в нуль. Напряженность размагничивающего поля Нc называют коэрцитивной силой.
Если увеличивать в обмотке силу тока обратного направления, то индукция магнитного поля в сердечнике будет возрастать тоже в противоположном направлении до насыщения. Далее, при уменьшении силы тока процесс размагничивания повторится. Кривую, описывающую этот процесс, называют петлей гистерезиса.
Магнитной цепью называется часть электротехнического устройства, предназначенная для создания в его рабочем объеме магнитного поля заданной величины и конфигурации.
Магнитная цепь электрических реле, трансформаторов, электрических машин состоит из источников, возбуждающих магнитное поле, и магнитопровода, в котором магнитный поток концентрируется и практически весь замыкается.
При расчете магнитной цепи может быть поставлена задача определения намагничивающей силы (н.с.) при заданном магнитном потоке или индукции — это прямая задача. Обратная задача — определить магнитный поток по намагничивающей силе.
В обеих задачах должны быть известны размеры участков магнитной цепи и кривая намагничивания материала.
Расчет магнитной цепи производится на основании первого закона Кирхгофа, по которому алгебраическая сумма магнитных потоков в узле магнитной цепи равна 0:
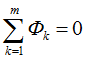
и второго закона Кирхгофа для магнитной цепи или закона полного тока
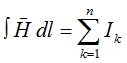
Циркуляция вектора напряженности магнитного поля Н по замкнутому контуру равна алгебраической сумме токов, охватываемых этим контуром.
Если контур интегрирования охватывает W витков, то
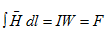 — намагничивающая сила или магнитодвижущая сила (МДС), измеряется в ампер-витках (ав).
— намагничивающая сила или магнитодвижущая сила (МДС), измеряется в ампер-витках (ав).
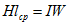
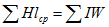
Закон Ома для участка магнитной цепи длиной 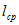 и площадью S. При напряжении
и площадью S. При напряжении 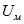 между концами участка связь между напряженностью магнитного поля Н и индукцией В выражается формулой:
между концами участка связь между напряженностью магнитного поля Н и индукцией В выражается формулой:
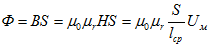
В этом выражении Ф аналогичен току электрической цепи, а магнитное напряжение — электрическому напряжению.
Тогда магнитное сопротивление
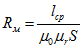
Магнитное сопротивление определяется воздушным зазором. При наличии воздушного зазора для создания соответствующей индукции требуется большой ток. При отсутствии воздушного зазора для создания соответствующей индукции требуется небольшой ток.
Нелинейность кривой намагничивания обусловливает нелинейность индуктивного сопротивления катушки на магнитном сердечнике.
Катушки индуктивности на ферромагнитном магнитопроводе считаются нелинейными элементами как в цепи постоянного тока, так и при синусоидальном напряжении.
Феррорезонанс
Для электрических цепей с нелинейным индуктивным и линейным емкостным сопротивлениями характерны явления феррорезонанса. При последовательном соединении различают феррорезонанс напряжений, а при параллельном — феррорезонанс токов.
Вольт-амперные характеристики электрической цепи при последовательном (a) и параллельном (б) соединениях
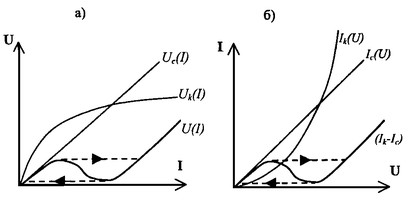
Скачкообразное изменение величины тока и его фазы при последовательном включении рассматриваемых элементов и скачкообразное изменение величины напряжения при параллельном включении являются одной из особенностей таких цепей. Релейные свойства феррорезонансных цепей используются в устройствах автоматики.
Схема последовательного соединения может быть использована в качестве стабилизатора напряжения.
Для изменения индуктивного сопротивления катушки с ферромагнитным сердечником используют подмагничивание сердечника дополнительной катушкой, питаемой постоянным током. В этом случае она называется дросселем насыщения и используется для регулирования скорости вращения двигателей, регулирования освещения, а также в выпрямительных установках с регулируемым напряжением.
Для чего нужен расчет магнитной цепи?
Задачей расчета в большинстве случаев является определение намагничивающей силы Iw, необходимой для того, чтобы возбудить в магнитопроводе определенный магнитный поток или определенную магнитную индукцию в некотором участке магнитной цепи (чаще всего в воздушном промежутке).

Схема расчета магнитных цепей.
Расчет ведется на основании закона полного тока, согласно которому сумма магнитных напряжений на отдельных участках магнитной цепи равна намагничивающей силе:
Здесь магнитным напряжением называется произведение напряженности поля Нk на длину соответствующего участка, т. е. Hklk.
Магнитная цепь делится по возможности на небольшое число n участков, в пределах каждого из которых можно принять напряженность H и индукцию В постоянными (на рис.1 п = 3). Затем, если задан магнитный поток Ф, для одного из участков, имеющего сечение S1, определяется магнитная индукция B1= ф :S1

Рисунок 1. Схема магнитной цепи с магнитным зазором.
А на основании значения магнитной индукции В1 с помощью кривой намагничивания ферромагнитного материала этого участка сердечника определяется напряженность H1 соответствующая индукции В1 (рис.2). В таком же порядке для второго участка нужно найти сначала В2=Ф:S2, а затем по кривой намагничивания H2. Таким путем последовательно определяется значение напряженности для всех n участков магнитной цепи.
Если в магнитной цепи имеется воздушный промежуток (или неферромагнитный участок), то сечение пути потока в воздухе можно принять равным сечению прилегающего ферромагнитного участка. Следовательно, индукция в воздушном промежутке Вв равна индукции на этом соседнем участке. На основании этой индукции определяем напряженность магнитного поля. Обычно в воздухе она оказывается довольно большой: Hв= Bв :µ 0,
Из-за того что магнитная проницаемость воздуха µвоз=µ относительно мала, и поэтому для возбуждения сколько-нибудь значительной индукции нужна большая напряженность поля.
Длиной каждого из участков магнитной цепи следует считать длину пути потока, т. е. длину средней магнитной линии.
После того как определено магнитное напряжение Hl для всех участков цепи, пользуясь законом полного тока, подсчитываем необходимую намагничивающую силу: H1l1+ H2l2+…+ Hвlв=Iw
При расчете полезно обратить внимание на то, что на маленький воздушный промежуток затрачивается большая часть намагничивающей силы.

Рисунок 2. График определения напряженности поля.
Если же нужно решить обратную задачу, определить магнитный поток или индукцию по заданной намагничивающей силе Iw, то расчет несколько усложняется из-за того, что неизвестно распределение напряженности Н между отдельными участками магнитной цепи, а оно зависит от неизвестной магнитной индукции. По этой причине задачу приходится решать путем подбора или посредством построения магнитной характеристики устройства. Нужно задаться некоторым вероятным значением магнитного потока Ф’ (или индукции для одного из участков) и рассчитать, как это было сделано выше, намагничивающую силу Iw’, необходимую для возбуждения этого потока. Полученное таким путем значение Iw’ следует сопоставить с заданным значением Iw. Если Iw’ существенно отличается от Iw, то нужно повторить расчет, задавшись новым значением потока Ф”; на основании этого расчета найти новое значение Iw” и т. д.
Кривая зависимости потока Ф от намагничивающей силы I w, построенная посредством таких расчетов, выполненных примерно для пяти значений Ф, будет представлять собой магнитную характеристику цепи. При помощи такой характеристики легко определить поток, соответствующий любому значению намагничивающей силы.
Для чего нужен расчет магнитной цепи?
Магнитная цель — это устройство из ферромагнитных сердечников, в которых замыкается магнитный поток. Применение ферромагнетиков имеет целью получение наименьшего магнитного сопротивления (3-21), при котором требуется наименьшая м. д. с. для получения нужного магнитного потока.
Простейшая магнитная цепь — это сердечник кольцевой катушки (рис. 3-11). Применяются магнитные цепи нерйзветвленные и разветвленные, отдельные участки которых выполняются из одного или из разных материалов.
Расчет магнитной цепи состоит из определения м. д. с. по заданному магнитному потоку, размерам цепи и ее материалам.
Для расчета цепь делят на участки  и т. д. с однородным полем, определяют магнитную индукцию
и т. д. с однородным полем, определяют магнитную индукцию  на каждом из них и по кривым намагничивания (рис. 3-18) находят соответствующие напряженности магнитного поля. Напряженность поля в воздушном зазоре или неферромагнитном материале
на каждом из них и по кривым намагничивания (рис. 3-18) находят соответствующие напряженности магнитного поля. Напряженность поля в воздушном зазоре или неферромагнитном материале

где Н выражено в амперах на метр, а в теслах, или  если Но выразить в амперах на сантиметр, а
если Но выразить в амперах на сантиметр, а  — в гауссах.
— в гауссах.
По закону полного тока сумма магнитных напряжений на отдельных участках равна м. д. с., т. е.

Пример 3-6. Сколько витков надо наложить на сердечник (рис. 3-20) для получения магнитного потока 47  при токе обмотки 25 А. Верхняя часть сердечника выполнена из стали
при токе обмотки 25 А. Верхняя часть сердечника выполнена из стали  а нижняя — из литой стали.
а нижняя — из литой стали.
Первый из трех участков из стали ЭЗЗО имеет длину  , сечение
, сечение  второй — из литой стали
второй — из литой стали  и
и  третий участок — воздушный зазор
третий участок — воздушный зазор  , сечение
, сечение 
Магнитные индукции на первом, втором и третьем участках:


Рис. 3-20. К примеру 3-6.
По кривой намагничивания для стали Э330 (рис. 3-18) индукции 1,3 Т соответствует напряженности поля 
Магнитное напряжение на первом участке

Напряженность поля для второго участка (рис. 3-18)

Магнитное напряжение на втором участке

Напряженность поля в воздушном зазоре

Магнитное напряжение на зазоре


Число витков обмотки  витков.
витков.
Расчет неразветвленной магнитной цепи
В неразветвленной магнитной цепи (рис. 3.12) если пренебречь потоком рассеяния, магнитный поток Ф во всех сечениях магнитопровода постоянен. Кроме того, в воздушном зазоре пренебрегаем явлением распора боковых магнитных

Рис. 3.12. Неразветвленная магнитная цепь
линий и для расчета используем основную кривую намагничивания ферромагнитного материала, т.е. пренебрегаем явлением гистерезиса.
При расчете магнитных цепей возникают две задачи: прямая и обратная.
В прямой задаче требуется найти магнитодвижущую силу м>1 обмотки, необходимую для создания в данной магнитной цепи заданного магнитного потока Ф, если известны размеры, конфигурация и материал магнитопровода, а также размеры и конфигурация воздушного зазора.
Решение задачи включает следующие этапы:
1. Разбиваем магнитную цепь на участки с постоянным сечением магнитопровода и определяем средние силовые линии участков 1к. Так, для магнитопровода (рис. 3.12) одинаковое сечение магнитопровода имеют участки аб (8Х) и бсс1а (52). Сечение воздушного зазора принимаем равным
 . Средние длины участков равны: для первого —
. Средние длины участков равны: для первого —  , для второго
, для второго 
2. Определяем магнитные индукции на участках магнитной цепи, учитывая, что магнитный поток в магнитопро- воде постоянен. Для цепи рис. 3.12 находим:

- 3. Определяем напряженности магнитного поля в ферромагнитном материале Я, в воздушном зазоре магнитопро- вода для ферромагнитного материала Н2 по кривым В(Н) и для воздушного зазора Я по формуле (3.14).
- 4. Определяем искомую МДС по второму закону Кирхгофа

В обратной задаче требуется найти магнитный поток Ф в данной магнитной цепи, если известны: значение магнитодвижущей силы /м> = число витков обмотки; размеры,
конфигурация и материал магнитопровода; размеры и конфигурация воздушного зазора.
Данная задача решается методом последовательного приближения. Задаются конкретным значением магнитного потока Ф, (определяемого на основе опыта расчетов магнитных цепей) и в соответствии с методикой решения прямой задачи находится значение МДС , обеспечивающее поток
Сопоставляется полученное значение с . Если К^Кзад, то берем Ф2 > Ф и еще раз решаем прямую задачу, находим МДС . Сопоставляем значение МДС Я2 с , и продолжаем решение, пока не получим при каком-то искомом потоке Фиск МДС отличающуюся от нее на небольшую величину МДС . Задача решается методом итерации на ЭВМ.
Магнитная цепь

Магнитной цепью называется устройство, отдельные участки которого выполнены из ферромагнитных материалов, по которым замыкается магнитный поток. Примерами простейших цепей могут служить магнитопроводы кольцевой катушки и электромагнита, изображенного на рис. 6.11, а. Электрические машины и трансформаторы, электромагнитные аппараты и приборы имеют обычно магнитные цепи более сложной формы.
 Рис. 6.11 Магнитные цепи (а — неразветвленная, б — разветвленная)
Рис. 6.11 Магнитные цепи (а — неразветвленная, б — разветвленная)
Если магнитная цепь выполнена из одного и того же материала и имеет по всей длине одинаковое сечение, то цепь называется однородной.
Если же отдельные участки цепи изготовлены из различных ферромагнитных материалов и имеют различные длины и сечения, то цепь — неоднородная.
Магнитные цепи, так же как и электрические, бывают разветвленные (рис. 6.11,6) и неразветвленные (рис. 6.11,а).
В неразветвленных цепях магнитный поток Ф во всех сечениях имеет одно и то же значение.
Разветвленные цепи могут быть симметричными и несимметричными. Цепь, представленная на рис. 6.11,6, считается симметричной, если правая и левая части ее имеют одинаковые размеры, выполнены из одного и того же материала и если МДС I1W1 и I2W2 одинаковы. При невыполнении хотя бы одного из указанных условий цепь будет несимметричной.
Разобьем неразветвленную магнитную цепь, например, на рис 6.11, а на ряд однородных участков, каждый из которых выполнен из определенного материала и имеет одинаковое поперечное сечение S вдоль всей своей длины. Длину каждого участка L будем считать равной длине средней магнитной линии в пределах этого участка. Из сказанного выше следует, что магнитные потоки всех участков неразветвленной цепи равны, т. е.
и поле на каждом участке можно считать однородным, т. е. Ф= BS; поэтому
Где n — число участков цепи. Магнитное напряжение на любом из участков магнитной цепи
Где H — Напряженность, (измеряется в ампер на метр А/М).
B — Магнитная индукция (измеряется в теслах Тл).
L — Длинна средне силовой линии проходящей через центр поперечного сечения магнитопровода.
S — площадь поперечного сечения магнитопровода.
 — Магнитная постоянная.
— Магнитная постоянная.
При заданном направлении тока в обмотке направление потока и МДС IW определяется по правилу буравчика.
Магнитное сопротивление и закон Ома для магнитной цепи.
По аналогии с электрической цепью величину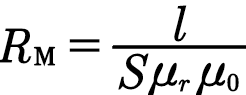
называют магнитным сопротивлением участка магнитной цепи (измеряется в 1/Гн).
Таким образом, магнитное напряжение Выражение (3) по аналогии с электрической цепью часто называют законом Ома для магнитной цепи Однако вследствие нелинейности цепи, вызванной непостоянством магнитной проницаемости μr ферромагнетиков, оно практически не применяется для расчета магнитных цепей.
Выражение (3) по аналогии с электрической цепью часто называют законом Ома для магнитной цепи Однако вследствие нелинейности цепи, вызванной непостоянством магнитной проницаемости μr ферромагнетиков, оно практически не применяется для расчета магнитных цепей.
Законы Кирхгофа для магнитной цепи
При расчетах разветвленных магнитных цепей пользуются двумя законами Кирхгофа, аналогичными законам Кирхгофа для электрической цепи.
Первый закон Кирхгофа непосредственно вытекает из непрерывности магнитных линий, т.е. и магнитного потока; алгебраическая сумма магнитных потоков в точке разветвления равна нулю: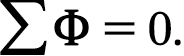
Например, для узла а на рис. 6.11,б
Второй закон Кирхгофа для магнитной цепи основывается на законе полного тока: алгебраическая сумма магнитных напряжений на отдельных участках цепи равна алгебраической сумме МДС: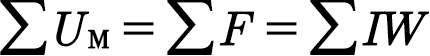
Например, для левого контура и а рис. 6.11, б Как следует из закона Ома, для получения наибольшего магнитного потока при наименьшей МДС у магнитной цепи должно быть возможно меньшее магнитное сопротивление. Большая магнитная проницаемость ферромагнитных материалов обеспечивает получение малых магнитных сопротивлений магнитопроводов из этих материалов. Поэтому магнитные цепи электрических машин выполняют преимущественно из ферромагнетиков, а участки цепей из неферромагнитных материалов, то есть неизбежные или необходимые воздушные зазоры, делают, как правило, возможно малыми.
Как следует из закона Ома, для получения наибольшего магнитного потока при наименьшей МДС у магнитной цепи должно быть возможно меньшее магнитное сопротивление. Большая магнитная проницаемость ферромагнитных материалов обеспечивает получение малых магнитных сопротивлений магнитопроводов из этих материалов. Поэтому магнитные цепи электрических машин выполняют преимущественно из ферромагнетиков, а участки цепей из неферромагнитных материалов, то есть неизбежные или необходимые воздушные зазоры, делают, как правило, возможно малыми.
Схема устройства магнитной цепи двухполюсной машины с явно выраженными полюсами показана на рис. 6.12.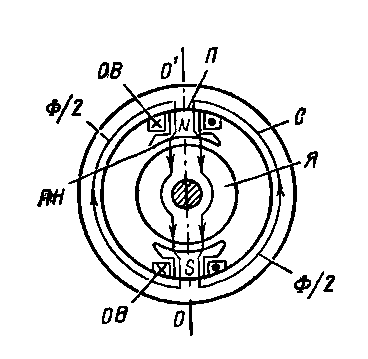
Рис. 6.12 Магнитная цепь электрической машины с явно выраженными полюсами
Плоскость 00′, проведенная через середины полюсов N и S и ось машины, делит магнитную цепь на две симметричные части. В каждой из них магнитный поток Ф/2 замыкается через полюсы П, полюсные наконечники ПН, воздушные зазоры, якорь Я и станину машины С. Магнитодвижущая сила создается током в обмотке возбуждения ОВ, расположенной на полюсах N и S. Из северного полюса N магнитные линии выходят и в южный полюс S входят.
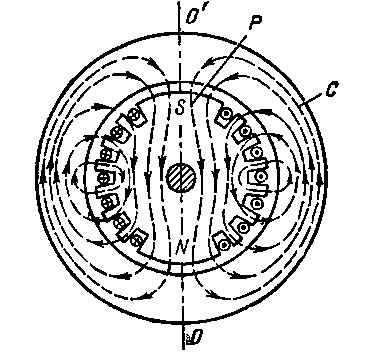
Рис, 6.13. Магнитная цепь электрической машины с неявно выраженными полюсами
Схема устройства магнитной цепи двухполюсной машины с неявно выраженными полюсами показана на рис. 6.13. Здесь обмотка возбуждения заложена в пазы ротора Р — вращающейся части машины, укрепленной на валу. Как и в предыдущем случае, плоскость 00′, проведенная через середины полюсов N и S, делит магнитную цепь машины на две симметричные части, в каждой из которых магнитный поток Ф/2. Магнитный поток замыкается через ротор машины, воздушные зазоры и станину машины С, представляющую собой неподвижный наружный стальной цилиндр — статор машины.


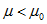 (висмут, вода, водород, медь, стекло);
(висмут, вода, водород, медь, стекло);
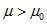 (кислород, платина, вольфрам, алюминий);
(кислород, платина, вольфрам, алюминий);
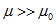 (железо, кобальт, чугун, никель).
(железо, кобальт, чугун, никель).

